Abstract
Over the course of one year, we systematically observed instruction in nearly all large gateway STEM courses at the University of California, Irvine to assess the prevalence of promising instructional practices and their implications for student success. More than half of the courses included promising instructional practices. Our most conservative student fixed-effects models suggest that students earn slightly higher grades in courses where instructors use explicit epistemological instruction, frequent assessment, and interactive instruction. Although we find no evidence to suggest that these strategies have lasting effects for the average UC Irvine student, we do find they have unique positive effects on the achievement of first-generation college students.
Global labor markets increasingly demand professionals with sophisticated skills in science, technology, engineering, and mathematics (STEM) (Lansiquot et al. 2011; Vergara et al. 2009). However, too few U.S. college graduates have these in-demand skills (Goldin and Katz 2009; Levy and Murnane 2012). Instruction in undergraduate STEM courses may be partly to blame, as many are organized into large lectures in which expert teachers transmit knowledge with minimal student interaction; it is argued that this course design contributes to attrition from STEM majors during the first undergraduate years (Baillie and Fitzgerald 2010; Kyle 1997; McGinn and Roth 1999; Mervis 2010; NAE 2005). In this study, we investigate the effectiveness of several instructional practices that have been proposed to reform large introductory STEM courses. Our study consists of one year of detailed observations of the instructional practices in forty sections of eight large introductory STEM courses at the University of California, Irvine (UCI). By linking these observations to administrative records of nearly five thousand undergraduates enrolled in these courses, we examine whether instructional practices identified as “promising” by leading national organizations influence students’ course grades, odds of enrolling in the next STEM course, and their grades in the subsequent course (Nielsen 2011). Our analyses provide a preliminary look at the relationship between widely implemented promising instructional practices and student outcomes using a student-level cross-course fixed-effects design to control for time-variant observable student characteristics as well as time-invariant student characteristics. We find that students earn slightly higher grades in courses that use promising instructional practices. However, we find no evidence that promising instructional practices have longer-term achievement effects across the entire student population, with the exception of first-generation college students, who may derive some post-class benefits from exposure to promising instructional practices.
We draw on reports from the National Academy of Sciences (NAS) and the National Research Council (NRC) in which promising practices were identified from a review of the research in undergraduate STEM education (Hake 1998; NAE 2005; Nielsen 2011; Wolter et al. 2011). We focus on three of the practices that figure prominently in the NAS/NRC recommendations: explicit instruction in epistemology or “thinking like a scientist,” formative and summative assessment, and group-based or interactive learning. Although these instructional practices have a strong theoretical basis and intuitive appeal, findings about the effectiveness of these practices remain unclear. In particular, much of the research supporting promising instructional practices comes from evaluations of highly motivated and trained instructors in low-enrollment course settings or larger, discipline-specific studies (NAE 2005; Nielsen 2011). To address this gap, we systematically observe instruction across a variety of STEM disciplines and link these observations to student-level administrative data. Taking advantage of the instructional variation that we observe across these courses, we estimate the relation between exposure to instructional methods and grades in observed STEM courses, enrollment in subsequent courses toward STEM degrees, and grades in subsequent STEM courses. By focusing analysis on students who are exposed to multiple instructional styles across different classes and observing the extent to which this within-student variation is associated with variation in sub-sequent persistence and success in STEM courses, our approach makes it possible to separate the effects of these instructional practices from potentially confounding student characteristics.
BACKGROUND
Demand for employees in STEM is projected to outpace demand for employees in other occupations (NSB 2010). However, the number of STEM graduates from U.S. higher education is not keeping pace (Felder, Felder, and Dietz 1998; NSB 2010). Furthermore, STEM employers report that too many recent graduates are poorly prepared for the problem-solving tasks required in real-world applications (NAE 2005; Vergara et al. 2009).
Efforts to reform undergraduate STEM education highlight the first two years of undergraduate education as a critical period (Tinto 2006; Upcraft, Gardner, and Barefoot 2005). During these early years, many American undergraduates are enrolled in large lecture courses. Although these courses provide an efficient mechanism for disciplinary experts to communicate information, they may fail to provide adequate scaffolding for students to engage, learn, and experience success. Given this, many argue that traditionally organized, large lecture courses are ineffective settings for facilitating the skill development required for persistence in STEM majors (Mervis 2010). Many colleges and universities have begun to promote more active and engaged learning in the interest of improving scientific understanding and retention in STEM disciplines.
Several studies estimate associations between instructional practices and student outcomes, including motivation and course satisfaction, test performance, content retention and recall, and mastery of conceptual reasoning and problem-solving skills (Colliver 2000; Newman 2005; Chaplin 2009; Knight and Wood 2005; Michael 2006; Dougherty et al. 1995; Gijbels et al. 2005; Strobel and van Barneveld 2009, 43; Antepohl and Herzig 1999; Crouch and Mazur 2001; Deslauriers, Schelew, and Wieman 2011; Dochy et al. 2003; Lansiquot et al. 2011). This literature provides broad guidelines for instruction based primarily on small-scale evaluations of promising instructional practices on specific student outcomes such as problem-solving abilities (Singer, Nielsen, and Schweingruber 2012; Deslauriers, Schelew, and Wieman 2011). For example, one experimental study, in which students were randomly assigned either to instructors trained to facilitate student interaction or to one of the control course sections, indicates that interaction improves students’ attendance, engagement, and conceptual knowledge (Deslauriers, Schelew, and Wieman 2011, 862).1 Although these results are encouraging and typical of other disciplines, the research literature is fragmented with little evidence assessing the extent to which practices effective in one discipline setting (such as physics) can successfully transfer to other disciplinary settings (Singer, Nielsen, and Schweingruber 2012).
Extant studies of promising instructional practices in introductory STEM courses commonly feature instructors with extensive pedagogical training and interest, showcased in courses with relatively small enrollments and rich instructional resources (Han and Finkelstein 2013). A meta-analysis of 225 studies found that active learning increases student performance in science, engineering, and mathematics. Student performance included examinations and concept inventories (N = 158 studies) and odds of failing the course (N = 67 studies) (Freeman et al. 2014). Although this meta-analysis provides no data on the size of the study courses or the degree of instructional training, it notes that results are stronger when class size is under fifty and that instructors in these studies volunteered to incorporate active learning pedagogies. These studies suggest that altered instructional practices in introductory STEM courses can substantially improve student outcomes, but they provide only limited information on how efficient these practices are when implemented at scale in more typical learning environments (such as lecture halls of two hundred or more) at a research university.
Furthermore, the existing literature provides limited information regarding the effects of promising instructional practices on students who are particularly at risk for attrition from STEM fields, including students who are the first in their families to attend college (Davis 2012; Nunez and Cuccaro-Alamin 1998). Only 20 percent of students from underrepresented groups who aspire to a STEM degree successfully graduate with one within five years; first-generation college students have lower undergraduate grade point averages (GPAs) and are less likely to persist in STEM than students of college-educated parents (Hurtado, Eagen, and Chang 2010; Vuong, Brown-Welty, and Tracz 2010; Ishitani 2006; Aspelmeier et al. 2012; Chen 2005; DeFreitas and Rinn 2013; Martinez et al. 2009). The first two years are crucial in narrowing the gap for these at-risk students; instructional practices may play a role (Chen 2005).
We evaluate three broad categories of promising instructional strategies implemented at scale in large lecture courses: teaching epistemology explicitly and coherently; using formative and summative assessments; and group-based or interactive learning. This work builds on a related study analyzing undergraduate survey data from the eight large University of California campuses, which found that cultures of engagement varied by major into two categories related to the purpose of the degree for upper division students (Brint, Cantwell, and Hanneman 2008). Our study uses data from course observations and syllabi to capture the extent to which instructors in lower division STEM courses implement these promising instructional practices and the impact they may have on student achievement.
The NAS identified “teaching epistemology explicitly and coherently” as a promising practice for undergraduate STEM instruction (Nielsen 2011, 24). We define epistemology as understanding the concepts, separating fact from opinion, and critically analyzing concepts (Goldman 1986). For example, instructors might teach epistemology by modeling problem-solving techniques during lecture and guiding analysis of concepts—sometimes referred to as “thinking aloud.” In other cases, they might teach epistemology by describing a key concept's intellectual history and its relevance to their research or to the field more broadly (DeLuca and Lari 2013; Pace and Middendorf 2004). Explicit coherent teaching includes systematically rearranging course content according to students’ epistemological awareness and metacognition and strategically addressing science misconceptions prevalent among undergraduates (Grant 2008). To illustrate, instructors can intentionally refer to prior course content and big ideas, provide reinforcement through exam content, and connect content with everyday experience, helping students reframe understanding.
The NAS report advocates use of structured evaluations to improve undergraduate STEM instruction “using formative assessment techniques and feedback loops to change practice” as well as “developing learning objectives and aligning assessments with those objectives” (Nielsen 2011, 24). Formative assessments offer immediate feedback to both student and instructor. This feedback allows instructors to modify their teaching based on current student understanding and allows students to modify their study strategies (Black 2013; Harlen and James 1997). Formative assessment occurs when instructors check for students’ understanding (via clicker questions and in-class exercises) and modify the lecture accordingly (Han and Finkelstein 2013). Instances of effective summative assessment include repeated use of graded exams, quizzes, and homework (Black 2013; Harlen and James 1997). These allow the instructor to ensure that learning objectives and assessments are properly aligned. Summative assessments also provide feedback so that students can modify their study strategies.
Interactive lectures provide opportunities for students to interact with peers and instructors (Singer, Nielsen, and Schweingruber 2012). Promising practices designed to improve interaction in lectures include: “allowing students to ‘do’ science, such as learning in labs and problem solving,” “providing structured group learning experiences,” and “promoting active, engaged learning” (Nielsen 2011, 24). Student-centered approaches create opportunities for students to collaborate over a single problem, or for more extended periods in a “flipped format” (Garcia, Gasiewski, and Hurtado 2011; Stage and Kinzie 2009). In addition to instructional reform, course structure reform—such as the addition of a lab section—provides added opportunity for collaboration (Nasr and Ramadan 2008; Farrior et al. 2007; Khousmi and Hadjou 2005).
METHOD
Our study uses systematic observations of instructional practice in large introductory STEM lecture courses from the Schools of Biological and Physical Sciences at UCI during the Spring 2013, Fall 2013, and Winter 2014 quarters. UCI is a highly selective institution and these schools are among the fastest-growing units on campus. Together, they enroll 55 percent of UCI undergraduates and 95 percent of UCI undergraduates in STEM fields. Enrollment for these schools has increased by 20 percent between 2003 and 2012. Over the same period, UCI's student population has undergone substantial demographic changes. Currently, 55 percent of UCI students are first-generation college students and 30 percent are members of underrepresented minority groups (UC Irvine Office of Institutional Research 2013).
Although more than 95 percent of UCI undergraduates earn a bachelor's of arts (BA) within six years, many students who begin as STEM majors transfer to other disciplines. After six years, fewer than half of incoming freshmen in the School of Physical Sciences earn a baccalaureate degree from that school, while retention rates of majors in Biological Sciences hover at approximately 60 percent (UC Irvine Office of Institutional Research 2013). In an effort to improve STEM persistence, both schools are undertaking instructional reforms. However, considerable instructional variation exists at UCI both across courses and even across sections of the same course. Course instructors have considerable discretion over their pedagogical methods. In many cases, lecturers—a category of instructors that includes adjuncts as well as teaching professors with security of employment—are leaders in the adoption of promising instructional practices.
By linking data from our observations of instruction in large gateway lecture courses with student-level administrative data, we take advantage of variation in instruction across sections of the same course to conduct a nonexperimental, population-based evaluation of the extent to which promising instructional practices promote positive student outcomes during the first two years.
Sample and Procedure
We observed instruction in forty introductory STEM courses at UCI. Our study identified all courses in the School of Biological Sciences and Physical Sciences that were prerequisites for other mandatory courses in one or more STEM major, were offered in multiple sections during the course of the year, and enrolled two hundred or more students. Eight courses met these criteria: Biological Sciences, From DNA to Organisms (BioSci 93), General Chemistry (Chem 1A, 1B, and 1C), Organic Chemistry (Chem 51A and Chem 51B), Single-Variate Calculus (Math 2A), and Classical Physics (Phys 7C).2 It is useful to note that the courses in our sample play somewhat different roles on campus. Introductory Biology (BioSci 93) is the first of several mandatory courses for the Biology major. Similarly, the general chemistry series and organic chemistry courses are required for several STEM majors. By contrast, a lower proportion of students are required to take the next course in the sequence for Mathematics 2A and Physics 7C. During the year of the study, the university offered forty-two sections of these courses; forty sections participated in the study. Trained research assistants observed one course session in the first three weeks and one course session in the last three weeks of regular instruction. An overview of the course sample is presented in table 1.
Description of Full Sample
For each observation, research assistants videotape lectures and collect data on instructional strategies using a researcher-developed observation protocol known as Simple Protocol for Observing Undergraduate Teaching (SPROUT).3 Observations include detailed field notes during the lecture that are subsequently transferred to the observation protocol and contain both dichotomous indicators and qualitative evidence. Two researchers overlapped on 20 percent of the course sessions with inter-rater reliability of Cohen's kappa = 0.80. Coding disagreements and ambiguities were discussed among the research team as they occurred during the data collection process. Course materials such as syllabi and key handouts are also collected to identify content related to epistemology, assessment, and interaction.
Student administrative data was collected from the Office of Institutional Research (OIR). Our sample is diverse—58 percent are first-generation college students, 26 percent are members of underrepresented minority groups, and 56 percent are female. In addition to demographic and academic data, OIR provides course enrollments and grades (both in observed courses and in courses that students take in subsequent terms), allowing us to track student progress toward STEM degrees. The sample consists of UCI freshmen and sophomores attending one or more focal (that is, observed) courses. As few transfer students enroll in these introductory courses, they are excluded from analysis. The total sample includes 4,801 students. Students can enroll in more than one of the observed courses; thus a single student can provide more than one case and the analysis file includes 11,803 distinct observations.
Measures
The present study considers the relation between instruction and three measures of student success: student grades in the observed course (measured on a four-point scale, where an A is 4.0 and an F is 0.0), student odds of enrolling in subsequent courses toward STEM degrees, and student grades in subsequent STEM courses.4 Course syllabi indicate that grades in these classes were not curved to the mean, but rather on a straight point scale (Carrell and West 2008). Each of the observed courses serves as a prerequisite for another course in the same field. For example, students are required to successfully complete BioSci 93 to enroll in BioSci 94. Our subsequent enrollment outcome is a dichotomous measure of whether the student completed the subsequent course during the next academic term.5 Our third outcome is the student's grade in that subsequent course, conditional on enrollment in the subsequent course and measured on a four-point scale.
We create composites for three instructional variables of interest: epistemology, assessment, and interaction. Items from observed lectures at both time points are summed to create a course composite measure. In these analyses, we assume that instructional practices are consistent across sections taught by the same instructor.6 Correlation tables for the variables between the first and second observation are included in appendix C. Because of the limited number of observed courses, a confirmatory factor analysis on the measurement model was not possible. As a result, we conceptualize our measures as indices or composites rather than as latent variables. The three measures capture the degree to which instructors engage in each of the three broad categories of instructional practices rather than indicators of how well instructors implement these practices (instructional quality).
The epistemology scale measures the extent to which instructors taught epistemology explicitly and coherently. We use five items from SPROUT to assess whether the instructor: models problem-solving techniques; makes connections between the course material and everyday student experience; refers to what students learned in prior course content; explicitly refers to themes, major theories, or other “big ideas” in the course; and refers explicitly to content on an upcoming exam. Summed across time points, epistemology practices range from 3 to 8 with a mean of 5.76 and standard deviation of 1.84 (alpha = 0.54). The correlation of the measure across both time points is 0.33. While some instructors engage in these activities relatively consistently across the instructional quarter, others refer to prior course content more in the beginning and “big ideas” at the end.
To measure assessment practices within the course, we use four items from SPROUT and four items from coded course syllabi. Assessment items include whether students take a quiz during study observations; whether instructor measures student understanding; whether instructor modifies lecture content as a result of measuring student understanding; number of clicker questions during the observed lectures; whether course has online homework; whether course has traditional homework; number of weekly quizzes; and number of exams. Across both time points, assessment practices range from 3 to 23 with a mean of 7.46 and a standard deviation of 5.28 (alpha = 0.70). The correlation of observed assessment practices across both time points is 0.69.
To measure instructional practices related to interaction, we use four items from SPROUT and one item from the coded syllabi. These include whether the lecture is interactive inclusive of student-peer or student-instructor exchanges; whether the instructor asks students to work in groups; whether work is conducted during the lecture; whether the course uses a flipped format; and whether a laboratory section is associated with the lecture. Across both time points, group-based or interactive practices range from 0 to 6 with a mean of 1.70 and standard deviation of 1.57 (alpha = 0.61). The correlation of group-based or interactive practices observed across both time points is 0.74.
To ease interpretation, we standardize the instructional variables and create z-scores. Because alphas of the constructs were relatively low, we estimate additional models using the individual items which constitute each of the scales. We note the results of these models when they are significantly different from zero in appendix B.
Where appropriate, analyses use demographic data collected from OIR, including gender (male or female), ethnicity (Asian American, African American, Hispanic, white, and other), first generation to attend college, and income status. Student academic characteristics are measured using weighted high school grade point average, mathematics and verbal SAT scores, and whether or not students took an advanced placement exam corresponding with the observed course. To ease interpretation, we standardize all continuous variables and create z-scores.
ANALYSES
The first analytic step involves descriptive investigation regarding the extent to which instruction and student outcomes vary across course sections. Observable student characteristics are associated with student exposure to three broad instructional variables, which may be a concern for interpreting the relation between exposure to instruction and academic outcomes.
After considering the student factors that predict exposure to promising instructional practices, we consider the relation between these practices and student achievement. We conduct a series of logistic and ordinary least squares regressions of the following basic form:
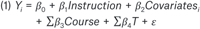
where Yi is the outcome of interest (odds of taking next course in STEM sequence). Instruction is the composite score for the specific instructional practice. Covariates represents a vector of student-level controls described above, including college enrollment year, transfer status, high school grade point average, SAT scores, gender, first generation to attend college, low income status, whether or not the student is repeating the course, and ethnicity. Course includes a matrix of course-title fixed effects designed to control for aspects of content, instruction, and student behavior that do not vary across sections of the same course.
We use a student fixed-effects model to more reliably identify the causal effects of instruction on grade in observed and subsequent course. This includes a high school fixed-effect term controlling for characteristics of high schools attended before matriculation at UCI. It may be that students from the same high school have similar preparation or prior knowledge that affects their performance, and to the extent that students from the same high school enroll together in the same sections of introductory-level courses, and that high school characteristics could confound analysis of instructional practices. These analyses take advantage of the fact that many students are enrolled in multiple courses that we observe. For example, typical first-year biology majors at UCI might enroll in as many as four observed courses (introductory biology, general chemistry, organic chemistry, and calculus). Repeated observations make it possible to account for observed and unobserved student characteristics and behaviors that are constant within a student, and thus more reliably estimate the extent to which exposure to promising instructional practices influences student academic behavior in that course and the subsequent course, net of observed and unobserved student characteristics (for analyses using a very similar design in public high school settings, see Clotfelter, Ladd, and Vigdor 2007; Xu, Hannaway, and Taylor 2011). These models take the following general form:

In this equation, Yij is the outcome of interest: student grades in focal course j and student grades in which focal course j is a prerequisite. Student in this model is a matrix of student fixed effects, controlling for all characteristics of students that are fixed across courses, including observable characteristics such as student race, gender, and economic and academic background, as well as invariant student characteristics such as intelligence and motivation.7 The parameter of interest in this model, Instruction, therefore estimates the extent to which exposure to a given instruction technique in a given course influences a student's achievement in that course (along with subsequent course) when compared with other observed courses also taken by that student.
Model 2 provides more internally valid estimates of the causal effects of exposure to instruction than model 1. To be included in the student fixed-effects model, students must take at least three observed courses, which ensures that students take courses in more than one discipline. For example, rather than just Chem 1A and Chem 1B, a student taking three or more courses might also take BioSci 93. Nearly half of the students meet this criterion and thus contribute to the student fixed-effects analyses. Although the students in the fixed-effects sample do not differ significantly from students in the whole sample on demographic characteristics, they do score higher on several measures of prior achievement and include more STEM majors than the full sample. Table 1 provides descriptive statistics for the full sample and table 2 provides descriptive statistics for the student fixed-effects sample.8 It is possible that the student fixed-effects model does not fully address the selection issues, because students may be more or less highly motivated by specific classes. However, by isolating instructional effects for individual students, it is the best approach to reliably identify the causal effects of instruction on observed and subsequent course.
Student Fixed-Effects Sample: Students in Three or More Observed Courses
In supplementary analyses, we add a series of instruction*first-generation student interaction terms to our student fixed-effects models. These interactions estimate the extent to which the association between instruction and student outcomes is different for students who are the first in their families to enroll in college compared with their peers who have more extensive exposure to higher education settings.
RESULTS
We include descriptive data on courses and instructional practices, followed by associations between these practices and student outcomes.
Instructional Variation Across and Within Courses
Table 3 provides a description of sample size by course, along with percent of students in each course who progress to the next course. Because these courses are effectively a program gateway, administrators and instructors meet regularly to discuss course syllabi, instructional materials, and content. These conversations limit instructor freedom to define course content, but instructors have considerable autonomy over instructional strategies.
Students Enrolled in Focal Course and Subsequent Course
Table 4 provides descriptive data for three instructional measures (epistemology, assessment, and interaction). Observed instruction varies in important ways across disciplines and courses. Because all biology and physics course sections use clickers, courses in these fields rate higher than courses in other disciplines on the assessment scale. Biology has the highest mean on the interaction index, whereas Chem 51A and Chem 1C generate the highest means on the epistemology scale. Chem 1B and Math 2A yield the lowest means for all three instructional measures.
Instructional Variation Across and Within Courses
Most instructional practices also vary substantially across sections within the same course. Although BioSci 93 course sections involve more interactive instruction on average than other courses, we observe considerable variation in the prevalence of interactive instruction among the six BioSci 93 sections. Indeed, the standard deviation for the interactive instruction among BioSci 93 students (1.41) is larger than that for interactive instruction in the overall sample (1.00). This variation across course sections is important for our identification strategy given that we include course fixed effects. Less variation is evident in the use of formative and summative assessments across course sections relative to the variation across course sections in interactive instruction and explicit instruction about epistemology. Indeed, for Chem 1C we observe no variation in the use of assessment across course sections. Such within-course homogeneity makes it particularly difficult to identify the effects of assessment on student outcomes.
Student Selection into Instructional Environments
Because we cannot randomly assign students to classes, values in table 5 show the extent to which observable student characteristics predict instructional strategies used in the classroom. These analyses include controls for course titles, which explain between 50 percent and 80 percent of the observed variation in instructional exposure.9
Selection by Observables with Course Fixed Effects
Exposure to explicit epistemological instruction and assessment do not seem to vary substantially with observable student characteristics. However, we find that men, Hispanic students, nonresident international students, and students retaking a course (after failing it) are exposed to more interactive instruction than peers, conditional on other observable characteristics. Students’ SAT math scores are negatively associated with exposure to interactive instruction after controlling for other student characteristics. This suggests that some at-risk students and students who previously failed tend to choose courses with relatively high levels of interactive instruction.
Associations Between Instruction and Student Outcomes
Figure 1 shows student rates of progression to the next course in the sequence after controlling for student characteristics. BioSci 93 has more than 85 percent of students successfully progressing to the next course in the program sequence, despite the fact that instructional practices vary considerably across biology sections. By contrast, we observe considerable variation in progression rates for students in Chem 1A and 1B (general chemistry) as well as Math 2A. In Math 2A, for example, we observe several course sections in which fewer than half of students progress to the next course in the sequence, as well as sections in which approximately 70 percent of the students progress to the next course in the sequence. However, many STEM majors are not required to take the subsequent course, Math 2B.
Probability of Taking Next Course in Series
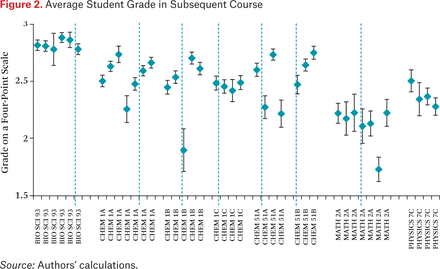
Figure 2 depicts the average grade earned in the subsequent course for those students who successfully progress, conditional on student characteristics. Grades prove to be relatively consistent in biology regardless of instructional practices for each section. This is not surprising as biology faculty standardized their grading. However, grades in chemistry and mathematics have larger standard deviations. Table 6 presents a series of analyses regressing student outcomes on instructional practices using the student fixed-effects sample (2,382 unique students; 4,762 observations). For external validity, we include analyses of the full sample in appendix C (4,801 students; 11,803 observations).
Average Student Grade in Subsequent Course
Effects of Instruction on Student Grades in Observed and Subsequent Course
Grades in the observed course
The first panel considers the link between instructional practices and student grades in the observed course. Whereas the first two models indicate no significant link between epistemology or interaction and student grades, the third model (including all controls) suggests that students achieve higher grades in courses higher on epistemology (0.024, p < 0.05). In particular, subsequent analyses (see appendix B) of the five items comprising the epistemology scale point to positive effects on course grades for drawing connections to the real world (0.034, p < 0.01) and highlighting the “big picture” (0.073, p < 0.05). However, problem solving has a negative effect on observed course grade (–0.072, p < 0.05). The third model also suggests that students achieve higher grades in courses with increased interaction (0.031, p < 0.01). Of the five items making up this scale, subsequent analyses show that lectures inclusive of student-peer or student-instructor exchanges point to positive effects on course grades (0.067, p < 0.001). All three models suggest a similar positive effect on grades for courses that use more assessments (0.048, p < 0.01). In particular, subsequent analyses of the eight items this scale comprises point to a strong relation between the use of whole-class checks for understanding and grades (0.085, p < 0.01), such as a clicker question or asking all students to respond by raising their hands. Grade in current course may be problematic, however, because there may be a relationship between instructional practices and instructor grading policies.
Course Progression
To consider the relation between instructional practices and student odds of progressing to the next course in the STEM sequence, we used the full sample (see appendix A). Because the outcome for this analysis is dichotomous (in which students who enroll in the next course in the instructional sequence take a value of 1 and students who do not take a value of 0), we observe little variation among students who enroll at UCI from the same high school and even less variation applies to a single student. Therefore, we are unable to estimate high school or student fixed-effects models considering the link between instruction and student progression. However, the multivariate models reported in appendix A indicate that students who enroll in courses with frequent assessment and high levels of interactive instruction are significantly less likely to progress to the next course in the STEM sequence compared with peers in courses with lower values of these promising instructional practices. However, subsequent analyses point to a strong positive relation between problem solving and odds of progressing to the next course (0.182, p < 0.01) (see appendix B).
Grades in Subsequent Course
Perhaps the most powerful indicator of the extent to which instruction influences students’ acquisition and retention is the association between instruction and grades in subsequent courses. These relations are presented in the second panel of table 6. The results from the third model indicate no relation between the three promising instructional practices and student achievement in subsequent courses. Supplemental analyses point to a positive association between problem solving in the current course and grade in the subsequent course (0.097, p < 0.01). Although suggestive, the multiple comparisons problem applies to these supplemental analyses, in which we test the effects of twelve instructional variables.
Table 7 provides some evidence to suggest that these instructional practices have differential effects for an important student subgroup—first-generation college students. We include an interaction term to allow the association between instruction and subsequent student achievement to vary between first-generation college students and peers with college-educated parents. We find that first-generation students experience significantly higher gains in subsequent course grades than their counterparts when exposed to frequent assessment (0.065, p < 0.01) and interactive instruction (0.057, p < 0.01), but not explicit instruction in epistemology.
Effects of Instruction on First-Generation College Student and Grade in Subsequent Course
DISCUSSION
This study aims to evaluate the effects of three widely agreed-upon promising practices—explicit instruction in epistemology or “thinking like a scientist,” formative and summative assessment, and group-based or interactive learning—as implemented at scale in large undergraduate introductory STEM courses (Nielsen 2011, 24). Small-scale studies and discipline-specific studies suggest these strategies have potential for improving student outcomes (Hake 1998; NAE 2005; Nielsen 2011; Wolter et al. 2011). However, in the current study, which investigates these practices in large undergraduate STEM courses typical of major research universities, we find little evidence to suggest that promising instructional practices improve student outcomes for the average UCI student. UCI is a single example and not generalizable to all undergraduate STEM universities. Yet the university is fairly typical of at least one important segment of the American higher education system—the large research university. Close examination of promising instructional strategies at this large, decentralized institution is capable of providing new insights regarding promising instructional strategies implemented at scale.
We use variation across sections of the same course to illustrate the effects of promising instructional practices on student grades in their current course, course progression, and subsequent grades. Our findings suggest that the relation between instructional practices and student outcomes is weak. Regardless of the extent to which instructors use promising instructional practices, student outcomes are fairly similar across course sections. Our most conservative student fixed-effects models suggest that students earn slightly higher grades in courses where instructors use explicit epistemological instruction, frequent assessment, and group-based or interactive learning. However, we find no evidence to suggest that these strategies have an effect on grades in subsequent courses for the average student. Furthermore, we find some evidence to suggest that first-generation college students benefit uniquely from exposure to frequent assessment and highly interactive instructional strategies.
Our findings also provide insights into the relation between instructional practices and students’ odds of progressing to subsequent courses in the STEM sequence. Although we are unable to estimate fixed-effects models on course progress, our multivariate models indicate that students exposed to frequent assessment and group-based or interactive learning are less likely to progress to the next course in the series than their peers in more traditional lecture classes. This finding raises important questions regarding the implications of promising instructional practices, implemented at scale, for improving student persistence in STEM fields. Future analyses should address the consequences of instructional practices for student persistence more extensively. Our findings—that the same instructional practices that predict high grades in a given course do not predict enrollment and success in subsequent courses—somewhat parallel Carrell and West's findings (2008). This study, which randomly assigned students to core courses at the U.S. Air Force Academy, finds that students who performed well in their initial mathematics course performed significantly worse in the mandatory subsequent courses in math, science, and engineering. Furthermore, they find that teacher effects are quite different between current and subsequent courses. Although students get lower grades, on average, in courses with high-ranking, highly educated tenured instructors, these same instructor characteristics positively predict student performance in subsequent courses.
However, two important caveats apply to these general findings. First, we find some evidence that two of the promising practices—exposure to formative and summative assessment and group-based or interactive instructional strategies—do benefit first-generation college students. These practices have a positive impact on grade in the next course in the STEM series. Given that first-generation students disproportionately drop out of STEM, this finding can be valuable for mitigating this attrition rate. Because we found no evidence that promising practices have a negative impact on the general population but a positive one for first-generation students, this may be an important consideration in their adaptation.
Second, our observational data focus on the extent to which instructors use particular strategies and not how well they implement thems. We suspect that this distinction is crucial. At UCI and in many other higher education settings, instructors have a great deal of professional autonomy, receive little pedagogical training, and have few signals regarding the effectiveness of their instruction and few incentives to invest considerable time and energy to teaching. After observing each of this study's courses, we conducted brief, informal interviews with each of the instructors we observed. We learned that many dedicated instructors refrain from implementing the sorts of promising practices that we highlight in this paper, choosing to stick instead with tried and true instructional techniques. Meanwhile, other instructors struggle to implement highly touted “promising practices” in an effective manner. We believe that future research and instructional reform efforts should devote attention to the processes through which instructors encounter and adopt promising instructional practices. In particular, we hope that the sorts of observational data our project has collected can help instructors reflect on their practices and learn from one another.
Third, UCI is a selective institution. At the time of this study, to enroll in introductory chemistry, biology, and mathematics courses, UCI students must either score above 600 on the mathematics portion of the SAT or complete a rigorous set of developmental math courses. Although our sample of UCI introductory STEM students is ethnically and economically diverse, these students are likely to be more motivated and academically engaged than their countparts nationwide. These characteristics may blunt the relation between instruction and student learning, insofar as UCI students’ study skills and motivation can compensate for courses with ineffective instruction. If true, it is possible that promising instructional practices have a larger impact among heterogeneous students enrolled in STEM courses at community colleges and other less selective colleges and universities, especially given that these colleges typically include more first-generation students who were found to benefit from the practices we observed (Wolter et al. 2011). Future research needs to address the effects of these promising practices at scale in heterogeneous settings, such as community colleges.
Acknowledgments
This material is based on work supported by the National Science Foundation under Grant Number 1256500.
APPENDIX A
Analyses of Full Sample
Effects of Instruction for Full Sample
APPENDIX B
Results of Analyses of Individual Scale Items
Effects of Statistically Significant Individual Items for Three Instructional Scales
Effects of Statistically Significant Individual Items for Three Instructional Scales
APPENDIX C
Correlations of Pre- and Post- Scale Items
Correlation Matrix for Epistemology Scale
Correlation Matrix for Assessment Scale
Correlation Matrix for Interaction Scale
FOOTNOTES
↵1. In the experimental section, 211 of 271 students attended the day of the test, versus 171 of 267 for the control section. All students were offered extra credit for their time.
↵2. Organic Chemistry is a three-course sequence. However, no specific course follows the third course in the sequence and so we included only the first two courses in our analyses, using the third only in our measures of course progression and subsequent course grades.
↵3. SPROUT adapted content from three well-known observation protocols: U-Teach Observation Protocol, or UTOP (Walkington et al. 2012); the Reformed Teaching Observation Protocol, or RTOP (Sawada et al. 2002); and Teaching Dimensions Observation Protocol, or TDOP (Hora and Ferrare 2014). SPROUT is available online at http://www.projectsprout.education.uci.edu (accessed February 23, 2016).
↵4. Although many studies on instructional practices use concept inventories or examinations, these were not available in this observational cross-disciplinary study.
↵5. The full sample was used to analyze whether students completed the subsequent course; the student fixed effects sample was used to analyze grade in observed and subsequent course.
↵6. We tested this assumption by observing multiple course sections taught by three instructors. These observations returned a high degree to consistency within instructors across classes, with observations of instructional practices correlating at the 0.93 level across sections.
↵7. Because student characteristics such as race and family background do not vary across course observations, model 2 excludes many of the student-level controls that our multivariate models include. However, the model includes controls for student characteristics that do vary across courses, including indicators of whether students completed AP courses relevant to the focal course and whether they are repeating the course.
↵8. All models use the Huber-White estimator to correct for clustering at the course section level.
↵9. Supplementary models using observable student characteristics to predict exposure to three instructional strategies (excluding course title controls) explain only 2 to 3 percent of the variance, but return similar relationships between student characteristics and instructional exposure.
- Copyright © 2016 by Russell Sage Foundation. All rights reserved. Printed in the United States of America. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Reproduction by the United States Government in whole or in part is permitted for any purpose. This material is based on work supported by the National Science Foundation under Grant Number 1256500. Direct correspondence to: Lynn C. Reimer at lcreimer{at}uci.edu, School of Education, University of California, Irvine, CA 92697; Katerina Schenke at kschenke{at}ucla.edu, National Center for Research on Evaluation, Standards, and Student Testing, University of California, Los Angeles, CA 90095; Tutrang Nguyen at tutrann{at}uci.edu, School of Education, University of California, Irvine, CA 92697; Diane K. O’Dowd at dkodowd{at}uci.edu, School of Biological Sciences, University of California, Irvine, CA 92697; Thurston Domina at tdomina{at}email.unc.edu, School of Education, University of North Carolina, Chapel Hill, NC 27599; Mark Warschauer at markw{at}uci.edu, School of Education, University of California, Irvine, CA 92697.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.