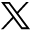Abstract
Using numbers of industrial robots shipped to primarily manufacturing industries as a supply shock to an industry labor market, we estimate that an additional robot reduces employment by roughly two to three workers overall and by three to four workers when robots are likely to be good substitutes for humans. The supply shock also reduces wages. The estimates far exceed those of an additional immigrant on employment and wages. While growth of robots in the 2000s was too modest to be a major determinant of wages and employment, the estimated effects suggest that continued exponential growth of industrial robots could disrupt job markets in the foreseeable future and thus merit attention from analysts and policymakers concerned about the economic well-being of workers.
Every week, the media reports on new developments in robotics or artificial intelligence (AI) that expand the ability of robots or computers to perform work traditionally done by humans. Diverse organizations ranging from academic think tanks to business consultants to national and international agencies have estimated the number of workers whose jobs are potentially at risk from advances in digitalization and robotization. 1 Although the estimated numbers vary by occupation, forecast period, and methodology, the headline message is clear: “Robots are coming and they are going to massively transform the world of work.”
Reacting to the headlines, researchers who look for clues to the future in past and recent labor statistics dismiss the forecasts of a job cataclysm as media hype rather than as plausible scenarios of the future (Mishel and Bivens 2017). Some note that all past automation scares failed to materialize. Historically, new technologies have invariably obsolesced some jobs but have also opened the door for new jobs, usually at higher pay and under better conditions. The occupational structure has shifted toward more skilled work, from farm laborers to factory workers to white-collar jobs in offices. Why should the most recent robotics technology differ drastically from past technological shocks?
Others note that the modest growth of productivity, the high level of employment to population, and the low unemployment rate after the recovery from the Great Recession are the opposite of what one would expect if technology were upending the world of work. To paraphrase Robert Solow’s (1987) observation about computers everywhere but in the productivity statistics, today we see robots taking jobs from humans in the media but not in real world labor markets. Reports that “the robots are coming” are not, however, about today’s labor market but about whether robotics technology has the potential to shake the world of work in the foreseeable future.
Our analysis addresses this question by examining whether the past two decades of exponential growth in the number of robots has left enough of a footprint on labor outcomes to support the concerns behind the media headlines or has had such a small impact as to validate the views of skeptical analysts. We treat the rapid deployment of robots in U.S. industries at the turn of the twenty-first century as a supply shock to the U.S. labor market and compare its effects on employment and wages to the effects of a more widely studied supply shock that also generates social concern— the entry of millions of immigrants over the same period.
Specifically, we combined data on the number of industrial robots shipped to each industry in the United States and other countries compiled by the International Federation of Robotics (IFR), with data on the number of immigrant workers by industry and state, and on employment and earnings of all workers, from the American Community Survey (ACS). Since 1993, the IFR has collected data on the shipments of industrial robots from the firms that produced those robots. The data are reported at the level of the industry that purchased the robots. We use the ACS to calculate the analogous influx of immigrants into those industries by state. Our analysis of employment and earnings outcomes rests on 19.5 million observations of individual workers between 2004 and 2016 for which the IFR reports sufficiently detailed industry figures to allow for a cross industry-time series analysis.
Because a firm’s decision to purchase robots and an immigrant’s decision of where to locate are likely to be influenced by labor-market conditions, we face a potential simultaneity bias in using ordinary least squares (OLS) to estimate the impact of robots or immigrants on employment and wages. On the company side, a higher wage should increase the firm’s incentive to invest in robots, imparting an upward bias in OLS estimates of the effect of the demand shock. To address this problem, we instrument U.S. purchases of robots using the number of robots shipped in the same industry and year in Japan and Germany in the IFR data. Ideally, this isolates the part of the growth of robots due to exogenous technological change that affects all countries similarly.
Immigrant choice of location and sector will also depend on labor-market conditions. We deal with the endogeneity of immigrant choice of working in a particular state and industry by using the 1970 distribution of immigrants from different sending countries by area and industry to create an instrument for current flows— a period sufficiently far from the 1990s and 2000s to provide a reasonably valid exogenous instrument.
We present three findings:
The influx of industrial robots into an industry over time is associated with a substantial fall in employment and earnings that is concentrated on less-educated workers and on those in occupations that experts view as automatable.
The entry of an additional robot reduces employment and wages by more than the entry of an additional immigrant, suggesting that one industrial robot is comparable to two to three human workers and upward of three to four in particular groups.
Although the number of robots per worker is too modest to be a major determinant of wages and employment patterns in the period covered by our study, our estimates suggest that continued exponential growth of robots could disrupt job markets in the next decade or so and thus merits monitoring and analysis by labor analysts.
Our empirical analysis has several weaknesses. Our measure of robotics technology is limited to industrial robots reported by the IFR, which follows the International Organization for Standardization (ISO) definition of robots, to be described shortly. The vast majority of industrial robots are found in manufacturing. We do not have data on other machines in manufacturing or elsewhere that may substitute for workers in the same way as robots but fall outside the ISO industrial robot classification, nor of service robots nor of software that can substitute for human workers in office or other digital settings. This biases our results toward finding robot effects on blue-collar workers but not on white-collar or service-sector workers.
In addition, the IFR data on the robot supply shock relates to units shipped to industries nationally and thus lacks geographic detail on the deployment of robots. This leads us to give each state an estimated number of robots proportionate to the state’s share of employment— creating measurement error in the robot variable in cross-state calculations. To the extent that the measurement error is random, this will bias our estimated coefficients on the impact of robots on labor-market outcomes toward zero. If firms in states with high or more rapidly rising wages or expansion of employment were induced by those conditions to invest more in robots than firms in other states, this would likely produce a positive correlation between robots and wages and employment, biasing our estimates of the impact on robots in a positive direction. We use an instrumental variables analysis to address these statistical problems.
Finally, the IFR data also do not record the particular types of robots that different industries purchase nor the price of those robots. Lack of this information is also likely to bias downward our estimated coefficients of the impact of robots on wages and employment.
MODELING ROBOT AND IMMIGRANT SUPPLY SHOCKS
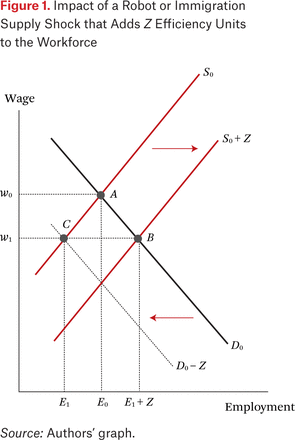
Changes in the number of robots or immigrants that substitute for workers can be analyzed as a supply shock that shifts the labor supply curve by the productivity equivalence between the robots or immigrants and the workers in the affected labor market. Figure 1 displays this point in a simple supply-demand framework in which a supply shock adds Z efficiency units to the workforce without affecting the demand for labor.
Impact of a Robot or Immigration Supply Shock that Adds Z Efficiency Units to the Workforce
Source: Authors’ graph.
If immigrants M have the productivity of θ existing workers, an increase in the number of immigrants by ΔM shifts the supply curve to the right by θ ΔM efficiency units so that Z = θ ΔM. This lowers the wage in the market and increases overall employment while reducing the number of workers exclusive of the new immigrants below the pre-shock employment level.
Similarly, if a single robot R has the productivity of γ workers, the supply shock due to a ΔR change in robots would change the number of efficiency units in the labor market by γ ΔR, so that Z = γ ΔR. The increased “employment” of efficiency units forces wages to fall to clear the market and reduces the employment of workers below its pre-shock level.2 If γ > θ, the increase of one robot has a larger impact on wages and employment of pre-shock workers than the increase of one immigrant.
Given that immigrants in a job market are likely to resemble existing workers in terms of their work skills reflected by education, age, or occupation, the equivalence parameter θ between new immigrants and existing workers is likely to be close to 1 (or modestly lower than 1 if the negative estimated coefficient on an immigrant dummy variable in a log earnings equation reflects productivity differences between immigrants and natives rather than discrimination against immigrants). By contrast, the equivalence parameter γ between robots and existing workers could differ greatly from 1 because technological change improves robot efficiency more than it does human efficiency. Implicit in the diverse forecasts of AI robots’ greatly displacing human workers is an assumption that γ is substantially greater than one, because a robot can do far more work than a human if only because it can operate twenty-four hours a day.
The impact of the two shocks on the employment and earnings of existing workers in figure 1—in which the numbers of robots and immigrants are measured in efficiency units—has a simple algebraic structure that guides our analysis. Measured as a vertical shift in the supply curve, the robot shock increases the “labor” supply as a percentage relative to the initial stock of workers L by γ (ΔR)/L, while the immigrant shock increases labor supply relative to L by θ (ΔM)/L. Let w be the wage of workers, σ be the elasticity of supply, and δ be the absolute value of the elasticity of demand. Then the impact of the two supply shocks on the total percent change in wages will be

Equation (1) shows that the impact of the two shocks is proportionate to their equivalent increase in the number of efficiency units relative to the size of the initial workforce. A regression of the change in wages on the change in the number of immigrants relative to base employment and on the change in the number of robots relative to base employment will yield a larger coefficient on robots than on immigrants if γ > θ and, conversely, if θ > γ. The contribution of the two shocks to the change in wages will also depend on the magnitude of the shocks. If, as turns out to be the case, the change in the number of immigrants exceeds the change in the number of robots in a particular period, θ ΔM could make a greater contribution to the change in the wage than γ ΔR even if γ > θ.
The effect on the size of the initial workforce is given by
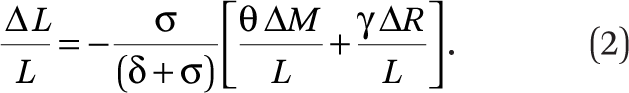
Both supply shocks reduce the number of current workers employed while increasing the total number of efficiency units and output in the industry. As with the wage impact, the difference between the two coefficients in equation (2) reflects the difference in the equivalence value of robots and immigrants with the existing workforce.
Our empirical analysis measures what happens to total employment (including immigrants) as a result of the robot and immigration supply shocks. The equation relating the change in the total number of workers to the supply shocks is

The impact of immigration on total employment will have a coefficient equal to one if the labor supply curve is inelastic (σ = 0), and will have a coefficient less than one if some of the initial workers (typically called natives) are displaced from their jobs.
This simple model provides the analytical framework for our empirical work. It is a schematic model that uses the equivalence framework to provide a clear interpretation of the calculations in terms of supply shocks, leaving aside factors that may further differentiate robot effects from immigrant effects (that is, different elasticities of substitution with existing workers across tasks, different complementarities with physical capital or R&D that also enter the production function, and constraints imposed by labor relations practices). The virtue of the supply shock framework is that it offers a way to examine the potential of robotic technologies to affect work relative to the benchmark of a shift in supply of workers captured by immigrants.
Measuring the Robot Shock
The key variable in our analysis of the labor-market impact of the robot shock uses data compiled by the IFR on the number of industrial robots shipped to firms by the producers of robots in a given year. About 90 percent of the machines in 2016 were purchased by manufacturing firms, the automobile sector being the lead industry and accounting for about half of the shipments.3
The IFR uses the International Standard Organization (ISO) definition of a robot (code 8373:2012) in its request for information from manufacturers. ISO defines an industrial robot as an automatically controlled, reprogrammable, multipurpose manipulator, programmable in three or more axes, which can be either fixed in place or mobile for use in industrial automation applications.4 The IFR reports shipments of robots for enough U.S. industries from 2004 to 2016 to allow us to estimate the impact of changes on employment and earnings using a time-series–cross-section design that exploits the variation in robot supply over time and across industries.
To get a sense of the types of machines included in the industrial robot category, the annual report of the IFR lists categories of applications that the robots perform.5 These include handling operations, machine-tending assistant processes for the primary operation, welding and soldering, dispensing, processing (where the robot leads the workplace or the tool in material removal), and assembling and disassembling.
These applications make it clear that industrial robots are likely to be direct substitutes for manual workers in factories—both skilled workers, such as welders, and less-skilled workers along an assembly line. They should have little direct impact on office workers or professionals, though impacts may spill over: a machine that reduces factory employment could, for example, shift white-collar employment from human resources to engineering.
The IFR survey collects data on the number of units shipped with no information on the price of robots or the value of shipments that could be used to generate an average price. The survey also does not provide any information on the specific attributes of the shipped products over time. The absence of value and attributes data rules out using the IFR survey to develop a hedonic price index that would transform the number of shipped units into a measure of effective units of fixed quality. Assuming that technological change improves the quality of robots over time, a fixed-quality measure of the number of robots would presumably grow more rapidly than the number of units reported by the IFR. If, for example, technological change improved the quality of each robot unit by 10 percent per year, the fixed-quality measure would increase by 10 percent more per year than the number of units. The number of robots sold is thus almost certainly a downward biased estimate of the effective supply of labor embodied in the machine.
The industry coverage of the IFR data varies over time. In the early years of the survey, the IFR reported a large unspecified category in its industry classification. Beginning in 2004, it gathered shipments by detailed industries for the United States that shrank the unspecified category substantially. We deal with the missing data problem by allocating the unspecified shipments in earlier years according to the 2004 industry share.
Because robots are a form of capital stock comparable to the capital stock of plant and equipment that enter standard production functions, the annual shipments have to be cumulated into a stock to measure their impact on output, wages, and employment.6 The IFR also produces an estimated “operational stock” of robots in a given year by summing shipments over the preceding twelve years with a depreciation assumption that “the average service life is 12 years and that there is an immediate withdrawal of the robots after 12 years.”7 Under this assumption, twelve years of shipments data are needed to obtain an estimate of the stock of robots in a given industry, which implies that a larger proportion of the estimated stock fits into the nonspecified category than of the estimated shipments, which substantially reduces the time series for analysis.
We deal with this problem by calculating our own estimates of the stock S of robots in an industry from the shipments data, applying the standard capital stock accumulation formula to the annual shipments. In particular, we write the stock of operating robots in year t, S(t), in terms of the depreciated pre-existing stock and the volume of new shipments, R(t), as
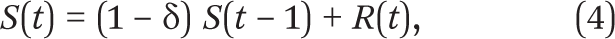
where δ is the depreciation rate, which could perhaps be on the order of 10 to 15 percent.
Equation (4), however, has a major problem. It ignores the likely improvement in the quality of robots over time. If robot manufacturers improve their product regularly, say by ψ percent per year, the number of quality-adjusted robots shipped in year t would be larger than the number shipped in year 0 even if the reported number of robot shipments were the same. Let R*(t) be the “effective” number of robots shipped in year t. The effective number of robots shipped in year t, relative to the number of robots shipped in year 0, would then be R*(t) = (1 + ψ)t R(t).
Taking account of both the depreciation of robot capital over time and its appreciation due to technological change yields the following equation defining the robot stock at time t:
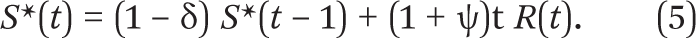
If depreciation were due solely to obsolescence, δ would be a function of ψ and the stock would depreciate or appreciate depending on the difference between the two values and the rate of investment in robots relative to the stock. Absent information on the rate of depreciation of robots and on the rate of appreciation of robot efficacy over time, we calculated the effects of robots under the simplifying neutrality assumption that the rate of depreciation and rate of appreciation roughly balance each other out.8 This makes our stock measure equal to the simple sum of the shipments to industries over time. We replicated our empirical analysis using alternative measures of a net depreciation rate (such as 10 percent) and obtained results that are similar to those reported below. The trend in the adjusted measures of the stock, regardless of the depreciation-appreciation rate assumed, is mainly driven by the rapid increase in the number of robots deployed by firms in the period studied.
Finally, the IFR data has no regional breakdown of shipments of robots within the United States. The lack of regional information is an important difference between our measures of the robot supply shock and the immigrant supply shock. Our econometric specification assumes that robots are distributed across areas within an industry proportional to employment in that industry.9 Without access to detailed data on the geographic distribution of robots, it is difficult to ascertain the potential biases introduced by this assumption.
Measuring the Immigrant Shock
Our data on the number of immigrants and on the employment and earnings of workers are drawn from the 2004–2016 American Community Surveys. We restrict our analysis to the sample of persons who worked at some point during the calendar year of each survey. We use the sampling weights reported in the ACS throughout the analysis, so that the weighted number of observations in our ACS sample estimates the size of the workforce.
Analyzing the link between the IFR’s reported number of robots in an industry and the ACS’s information on an industry’s employment and earnings requires a crosswalk between the industry classifications in the two data sources.10 Comparing the classifications, we developed a crosswalk that matches twenty-six industries, encompassing the entire workforce. Table 1 lists the industries and reports the total employment in each in the latest (2016) ACS cross-section. Because industrial robots are used primarily in manufacturing, the IFR distinguishes manufacturing industries in some detail and places most other workers in a residual category labeled as “all other non-manufacturing branches.” This residual category made up almost 68.4 percent of the workforce in 2016. Given this uneven distribution of workers across industries, we performed a regression analysis that excluded the residual category from our calculations. Despite its size, the exclusion of this industry from the analysis does not change the key results, primarily because this industry has effectively no data on robots and thus adds little information about how robots impact labor-market outcomes.
Summary Statistics in 2016, by Industry (Ranked by Robot Intensity)
We define our measure of robot intensity in an industry-year cell as the ratio of the stock of robots to the number of workers in the industry. In particular, let Si(t) be the stock of robots in industry i in year t; and Li(t) be the number of workers in that industry. We define the robot intensity index as

Table 1 shows that robot intensity varied substantially among industries in 2016. The industries with the highest intensity are computers and peripheral equipment, which has a robot intensity index of 15.9 percent, and automotive, with a robot intensity index of 12.3 percent. In contrast, the robot intensity measure in many other industries, ranging from agriculture, forestry, and fishing, to textiles to construction, is near zero.
We measure the immigrant supply shock by defining an immigrant as a person residing in the United States who is either a naturalized citizen or a noncitizen. The ACS also reports the immigrant’s year of arrival in the United States, which allows us to define the number of immigrant workers who arrived in a particular year, an annual flow comparable to the IFR data on the annual shipments of robots. We define the number of new immigrants in the ACS survey in year t as the number of immigrant workers who reported they arrived in year t–1.11 The immigrant stock is the total number of immigrants working in that year and reflects the most recent year’s flow of immigrant workers and any changes in the number who came earlier.
Our measure of the immigrant shock is the immigrant share of workers in a state-industry-year cell. In particular, let Mis(t) be the number of immigrants in industry i, state s, and year t; and let Lis(t) be the corresponding number of workers in that cell. The immigrant share is defined by

The third column of table 1 reports the immigrant share at the national level. It shows that the immigrant supply shock ranges from about 10 percent in mining and quarrying, basic metals, and automotive, to about 25 percent in construction, computers and peripheral equipment, and food and beverages and peaks at 30 percent in agriculture and nearly 35 percent in textiles.
We also use the ACS data to measure the number of workers and the earnings of workers in each industry-state-year cell. The employment measure is the total number of workers adjusted by hours of work.12 The earnings measure is the ratio of a worker’s wage and salary income to annual hours worked, which we refer to as hourly earnings. To better approximate changes in the price of skills, the earnings analysis is restricted to workers age twenty-five to fifty-nine who are not in school. Further, to avoid the contamination of hourly earnings trends by changes in sample composition between immigrant and native-born workers, the earnings analysis uses only the sample of native-born workers. Finally, because of potential measurement error, we excluded from the earnings analysis all workers who report hourly earnings in the bottom 1 or top 1 percentile of hourly earnings.13
ESTIMATING EFFECTS OF ROBOT AND IMMIGRATION SHOCKS
We used the merged IFR and ACS data on robots, immigration, employment, and wages to estimate the impact of the two supply shocks on labor-market outcomes. We begin with OLS estimates of the wage and employment equations and then turn to instrumental variable (IV) estimates that seek to identify the effect of robots and immigrants on wages and employment corrected for the simultaneous decision of firms to deploy robots and immigrants to supply labor to an area-industry. We exclude the (large) residual industry of all other nonmanufacturing branches defined by the IFR in the regressions as providing little insight into the effect of the industrial robots in the IFR data.14 Throughout the analysis, we estimate the regression models for all workers, for workers divided into three education groups, and for men and women separately.
OLS Estimates
To estimate the impact of the two supply shocks on the hourly earnings of workers, we aggregated the individual-level data in the ACS to the level of an industry-state-year cell, and calculated the mean skill-adjusted log hourly earnings in each cell. We first estimated earnings regressions at the individual level on a vector of variables giving the worker’s age, gender, and educational attainment. The residual from this regression gives the worker’s skill-adjusted wage. The mean skill-adjusted wage in a state-industry-year cell is then given by the average residual among workers in that cell. The second-stage regression model is given by
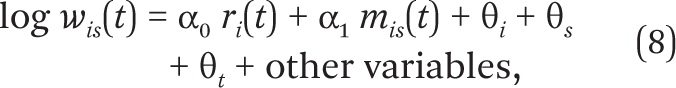
where θi gives a vector of industry fixed effects, θs gives the vector of state fixed effects, and θt gives a vector of year fixed effects. The coefficients of the robot and immigrant intensity variable capture the impact of the supply shocks on the “average” worker after standardizing for socioeconomic characteristics. To avoid composition effects due to the changing immigrant population, the earnings regression uses only the sample of native workers. The standard errors in the regression are clustered at the state-industry level.15
Table 2 presents OLS regression estimates of the impact of robots and immigrants on log of hourly earnings. The first column’s estimates for the full sample of workers shows a markedly larger and statistically more significant negative impact of robots per worker on earnings than of immigrants. This pattern replicates with differing magnitudes in all of our regressions with hourly earnings as the dependent variable. Interpreted as indicating the differing equivalence of robots and immigrants for existing workers in our model, the larger coefficient in the regressions on the number of robots than on the number of immigrants implies a larger equivalence parameter for robots, or γ > θ.
OLS Estimates of the Impact of Robots and Immigration on Log Hourly Earnings, 2004–2016
The estimates in the next three columns present the coefficients and standard errors from regressions for workers in specified education groups. They also show a pattern that will replicate with differing magnitudes in ensuing calculations—a larger estimated impact of robots on the least educated group than on the more-educated groups and a negative estimated impact of immigrants on the wages of the least skilled workers with a positive impact on the most skilled. This pattern of coefficients likely reflects the extent of substitution and complementarity between the different skill groups of natives and the typical immigrant. The immigrant population in the past two decades has been disproportionately low skill, hence the reduction in the wage of the least skilled natives and the modest positive impact on the wage of the most skilled natives. The OLS results are broadly consistent with the modest negative effect of immigration on the average worker and larger negative effect on the least skilled found in many immigration studies (Blau and Mackie 2016).
The final two columns present the results for women and men separately. They show modest gender differences in the relation of robots to earnings and a larger impact of immigrants on female earnings than on male earnings— a pattern that does not replicate in other calculations.
To estimate the impact of robots and immigrants on employment, we again aggregate the individual ACS data to calculate the size of the workforce in an industry-state-year cell as described earlier. The analogous regression model is then given by

where L is(t) gives the total number of workers (both natives and immigrants) employed in industry i, state s, at time t. We also conducted the aggregation separately for three education groups, and use these as alternative dependent variables. The regressions are weighted by the number of observations in the state-industry-year cell and the standard errors are again clustered at the state-industry level.16
Table 3 reports the estimated coefficients and standard errors for the robot and immigrant shock variables on employment. Because the dependent variable gives total employment in the industry-state-year cell, and includes immigrants, the baseline value of the coefficient of the immigrant supply shock is equal to one. Thus it is deviations from 1.0 in the estimated regression coefficient that tell us whether immigration led to a crowding out of the existing native workers.
OLS Estimates of the Impact of Robots and Immigration on Log Employment, 2004–2016
The estimated regression coefficient in table 3 linking employment to robot intensity is negative, which in conjunction with the negative estimated coefficients of robots on wages in table 2 supports our schematic model that treats robots as shifting the supply curve of equivalent labor. Viewing the estimated coefficient on robots as estimates of the human worker equivalence of robots, the column 1 regression suggests that one robot does the work of about two workers. The estimates for the different education groups show a slightly larger negative effect of robots on less-educated than on more-educated workers, though the differences are not statistically significant. The estimates by gender show a larger impact on female workers than on male workers.
The estimated coefficient of the immigrant intensity variable on employment of all workers is +0.80, which is modestly below the no-change baseline of 1.0. It suggests that an additional immigrant increases the total number of workers by 0.80 persons, which effectively reduces the number of native workers by 0.20 persons.
The regressions for education groups yield smaller coefficients for persons with twelve to fifteen years of schooling and sixteen or more years of schooling, which imply larger displacement of existing workers. But the large positive coefficient of the immigration variable for the least educated workers is anomalous. The anomaly arises partly because the small samples for this low-skill group in many of the state-industry-year cells force us to exclude many of the cells from the log employment regressions, while small numbers in non-empty cells add substantial measurement error to those cells. The small sample size reported in the regression for the least educated workers reflects the fact that more than 15 percent of the potential cells are empty (yielding an estimate of zero measured employment) relative to only 5.8 percent for workers with twelve to fifteen years of education. The small sample problem persists even in the cells that have a positive number of observations. In half of the cells for the least educated workers, our estimate of total employment is based on a sample of fewer than eleven persons. In contrast, the median number of observations in the non-empty cells for workers with twelve to fifteen years of education is seventy-four.
The small sample size in many cells, therefore, introduces a great deal of volatility in measured employment both within and across state-industry groups, particularly for the low-skill workforce. This sampling issue also partially affects the calculation of the immigration intensity variable for the state-industry-year cell, as the immigrant share is also calculated from the ACS data. In short, measurement error contaminates both the dependent variable (log employment in a state-industry-year-education cell) and the regressor measuring the immigration supply shock, generating a potentially severe bias because the number of working immigrants in a cell appears on both sides of the employment regression equation.
One way to reduce the spurious correlation is to estimate the regressions using the log number of working natives as the dependent variable. Although this specification does not measure the impact of robot intensity on total employment (after all, robots affect the employment of both immigrants and natives), the measured impact of immigration on low-skill employment should be less contaminated by the measurement error. Table A1 reports the regression results using this alternative dependent variable. The coefficients of the robot intensity variable resemble those obtained when using total employment as the dependent variable, but the OLS coefficient of the immigration intensity variable for the least educated workforce, while still positive, falls dramatically, indicating that the anomalously high coefficient for that group reported in table 3 reflects measurement error due to sample size.
Dealing with Simultaneity
Treating robots and immigrants as exogenous factors that shift the equivalent supply of labor in a market ignores the likely impact of labor-market conditions on the firms’ introduction of robots to an industry and on immigrants seeking work in a particular area and industry. The decisions of firms should produce a positive relation between wages and the number of robots as high wages induce firms to substitute more robots for workers.17 Similarly, high earnings in an industry-area are likely to attract immigrants to the industry-area. In both cases, the endogenous decisions to purchase robots or to immigrate will create a positive relation between the numbers of robots or immigrants and wages, biasing downward OLS estimates of the negative effects of the shocks along a given demand curve we seek to identify.
We deal with the simultaneity problem through a two-stage instrumental variable analysis. We instrument shipments of robots on the number of robots shipped in the same industry and year in Japan and Germany as reported by the IFR. Ideally, this isolates the part of the growth of robots due to exogenous technological change and economic conditions that affects the same industry in all advanced countries similarly. Given that Germany and Japan are leaders in robot technologies and top exporters of robots in the world,18 including to the United States,19 the instrument seems well suited to identify the part of U.S. purchases due to the supply shift of robots globally.
We deal with the endogeneity of immigrant choice with a variant of the shift-share instrument widely used in the immigration literature. We first calculate the state-industry distribution of immigrants who originated in a specific country in the 1970 Census. The key assumption is that this initial placement influences the state-industry distribution of later waves of immigrants from that same country, perhaps because of network effects. We allocate current immigrants from each country across the state-industry cells according to the country’s 1970 state-industry distribution. We then obtain the predicted number of current immigrants in each state-industry cell as the sum of the predicted number across all national origin groups. To the extent that the conditions that encouraged immigrants in 1970 to “settle” in particular cells persist over time, the instrument does not fully address the endogeneity problem. David Jaeger, Joakim Ruist, and Jan Stuhler (2018) examine the resulting biases and propose alternative methods of addressing the persistent endogeneity.20
Table 4 presents the IV estimates of the impact of the robot and immigration supply shocks on the log hourly wage. Consistent with the notion that simultaneity produces a positive bias on estimates of the impact of robots on earnings, the table 4 estimated coefficients are almost all more negative than the comparable table 2 OLS estimates. The IV estimated impact of an increase in robot intensity for all workers, for example, increases the effect on wages from –0.98 in table 2 to –1.21 in table 4. The sole exception is the coefficient on robots for college graduate workers, which becomes more positive, indicative of complementarity rather than substitution between the robots and the most highly educated group. The estimated coefficient on immigrants in the table 4 IV regression also becomes more negative than in the corresponding table 2 OLS regression. In the sample of all workers, the insignificant OLS effect of –0.05 turns into a –0.39 significant effect.
IV Estimates of the Impact of Robots and Immigration on Log Hourly Earnings, 2004–2016
Finally, replicating the OLS finding, the estimated IV coefficients on robots are substantially larger than those on immigrants, which in the context of our supply shock model suggests that the efficiency value of a robot exceeds that of an immigrant. For all workers, the effect of robots on the wage is about three times larger than the effect of immigrants on the wage, so that if an immigrant has approximately the same productivity of a native worker, a robot is equivalent to three workers.
Table 5 presents IV estimates of the impact of robots and immigrants on employment. The estimated coefficients for all workers are more negative compared to the corresponding estimates in table 3. The estimated negative coefficient on robots increased in absolute value for all workers from about –2.2 to –2.5 and increased a bit more in some of the least skilled groups. The IV estimate of the immigrant shock on total employment changes from the 0.80 found in the OLS regression to a coefficient of –0.19, which implies a more sizable displacement of the current workforce from the 1.0 neutrality (although the standard error is large). But as in the OLS regressions, we get an anomalous result for the least educated group of workers with an estimated coefficient that is larger than one (though not statistically different from one). Per the earlier discussion, we attribute this to the measurement error that arises from the large number of industry-state-year cells that were excluded from the analysis and to the small sample size in many other cells. As Table A1 shows, the use of the log of native employment as the dependent variable shows a crowding-out effect of immigration on native workers in all education groups, the adverse effect being larger for natives with less than a college education.
IV Estimates of the Impact of Robots and Immigration on Log Employment, 2004–2016
Bringing Occupations In
The media reports and projections of robot effects on jobs focus on how robots substitute for people in particular occupations or work tasks—ranging from assembling items along an assembly line, or spraying paint, or conducting surgery, and so on. The projections of Carl Frey and Michael Osborne (2013, 2017) that gained widespread attention for the claim that 47 percent of all U.S. employment was at risk of being computerized was, for example, based on an analysis of the probability that work would be computerized in 702 detailed occupations. Most other projection studies have similarly built their analysis on the basis of how technology is expected to affect occupations, not on industry purchases of robots (as in our tables 2 through 5).
That firms in any given industry hire workers in many occupations, some of whom may be affected by robots or other technological changes while others may not, creates a disconnect between the occupations/work tasks analysis and the industry analysis. The occupation data have an occupation subscript regardless of industry and our robot sales data have an industry subscript but no occupation subscript. To some extent, the limitation of the IFR data to industrial robots that primarily affect blue-collar workers and our exclusion of the all other nonmanufacturing branches part of the IFR data bound the occupation-industry problem by focusing on manufacturing. Still, our estimate of employment and earnings at the industry level almost surely understates the impact of robots on the subset of occupations within an industry whose work the robots are designed to perform. For instance, industrial robots could replace nearly all the welders in automobile production but have no effect on office workers in the industry, so that the effect on total employment would understate the impact on the workers actually given the “robot treatment.”
To bring occupations into our analysis, we examined measures of the characteristics of occupations from the U.S. Department of Labor’s Occupational Information Network (O*NET) data set, which measures the attributes of hundreds of occupations along diverse dimensions. 21 From the huge array of O*NET measures of occupational attributes, we selected one statistic as being most likely connected to robotization. This is the degree of automation of occupations that scores the extent of automation in an occupation on a scale from zero (no automation) to one hundred (most automated). 22 An industry with a large influx of robots is more likely to have a supply shock for occupations with greater degrees of automation than occupations the O*NET data views as relatively immune from automation. Similarly, the high automation occupation should have a greater supply shock in an industry with a large robot shock than in one with a modest increase in robots.
To incorporate the automation variable in our data, we attached to every worker in the ACS file the score of their occupation on the O*NET automation scale and then divided the occupations into three groups: those in the top quartile of the index (high automation); those between the 25th and 75th percentile of the index (medium automation); and those in the bottom quartile (low automation) of the O*NET index.
To the extent that the O*NET categories correctly identify the proneness of occupations to automation and that the robots contribute to automation, the regression of wages and employment on robot intensity should give large coefficients on robots for occupations in the top automation quartile and small coefficients on robots for occupations in the bottom quartile. This is effectively a double difference methodology that identifies robot effects by comparing wages and employment in automatable occupations in industries with large numbers of robots compared to workers in the least automatable occupations in industries with few robots. By contrast, we expect no clear pattern of differences in coefficients on the immigrant supply shock across occupations varying by the automation variable.
Table 6 summarizes the results from this analysis. It shows larger estimated negative effects of robots on hourly earnings and employment for workers in the top automation quartile group than in the lowest automation quartile. Estimates of robot effects for the middle group are closer to those of the top quartile group: a bit larger in the wage regressions but a bit lower in the employment regression. Both the earnings and employment regressions show a larger negative effect of immigrants for the high automation group, suggesting that some occupations experienced both a technology and immigrant shock.23
Estimates of the Impact of Robots and Immigration, by O*Net Degree of Automation in the Worker’s Occupation, 2004–2016
Given the attention given to the Frey and Osborne (2013, 2017) analysis of the likelihood of computerization of work on the future of jobs, we also examined the relation between their probability of computerization, which they derived making extensive use of O*NET data, on earnings and employment. We transformed their 702 occupations into a smaller grouping consistent with the ACS occupational category and found that their measure was positively correlated at 0.30 with the O*NET automation variable, suggesting that the two variables were capturing somewhat similar attributes of occupations. Some of the difference between the measures is presumably due to automation’s having primarily affected manual jobs in the past, whereas the impact of computerization extends to white-collar jobs. We then categorized occupations into the upper quartile, middle two quartiles, and lowest quartile of the probability of computerization of work.
Table 7 presents the OLS and IV regression coefficients on wage and employment equations for the three groups of occupations. As in our other calculations, the estimated robot effects are considerably larger than the estimated immigrant effects and become more negative with the IV analyses. The estimated effects of robots differ between the O*NET automation variable and the Frey and Osborne Probability of Computerization. The estimates presented in table 7 show that increased robot intensity reduced employment and wages even for workers in occupations having low probability of computerization.
Estimates of the Impact of Robots and Immigration, by Frey-Osborne Probability of Computerization in the Worker’s Occupation, 2004–2016
In short, dividing the data by attributes of occupations confirms our basic findings that an increase in one robot reduces wages and employment more than an increase in one immigrant does and gives plausible patterns across the groupings. The variation in occupational attributes beyond automation and computability suggests the value of investigating the link between those other occupational attributes and the impact of industrial robots on employment and wages. Table A1
CONCLUSION
Treating the deployment of industrial robots as a supply shock in a demand-supply model that includes the influx of immigrants as a separate measure of changes in supply offers a unique perspective on the development of technological substitutes for labor. It highlights the critical importance of the displacement parameter that connects the numbers of robots to the shift in supply of equivalent workers and provides a natural comparison metric in terms of the shift in supply due to immigrants. In our calculations, robots reduced wages and employment overall and in most groups, with substantially larger effects than that of immigrants. Taking the table 4 and 5 IV calculations for all workers as the best estimate of the overall impacts, the displacement effects of robots are on the order of two to three times the effects of immigrants. Honing down to narrower groups suggests that the impacts are larger for less-educated workers, for female workers, and for workers in occupations viewed as more automatable, ranging upward to robot displacement effects of three to four times.
Our estimated effects on wages and employment in the United States are close in magnitude to the estimates of Daron Acemoglu and Pascal Restrepo (2017), who examine the IFR data in a shorter period with a different methodology. They organized the data into commuting zone areas with the robot shock dependent on the industry mix in the area rather than on effects within impacted industries. That two different empirical approaches yield the same qualitative and similar quantitative results, robots reducing employment and wages for the most highly affected groups, suggests that the finding is “in the data” rather than in any particular modeling structure.24
Finally, our analysis provides a useful way to bridge the disagreement between the skepticism of traditional labor-market analysts, who regard fears of robot or other technologies impacting the job market as speculation with no evidentiary backing, and the analysis and projections by more technologically oriented researchers that warn of future labor-market dislocation.
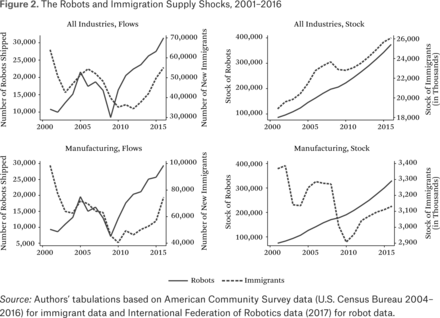
On the one side, our comparison of the magnitude of the robot shock and the immigrant shock in figure 2 supports the skepticism of labor analysts. Despite the media uproar about robots, the robot supply shock has been too modest through the mid-2010s to disrupt the labor market.
On the other side, the evidence that the increased supply of industrial robots has depressed employment and wages in affected industries, a robot adding the equivalent of two to three workers to labor supply on average and three to four workers in particular groups, suggests that it would be foolhardy to dismiss the concerns about the future of work. Reasonably large supply shock effects of technology and exponential growth of robots and related technologies have the potential to shake up the world of work in the foreseeable future.
To predict the effects of robots or indeed any other form of technological change or investment in machines that alters the world of work over the longer term requires analysis of how the technology affects the comparative advantage of workers over machines. In a market-clearing model, this is likely to have a greater impact on the structure of wages than on employment as workers displaced by the technology find other jobs and as the technology creates new forms of work and potentially raises the rate of economic growth enough to absorb any employment lost to machines.
Finally, since our data are limited to industrial robots, we do not examine thus treat the possible impact of service robots or of other type of machines (automation writ large) that can also affect the world of work. These limitations notwithstanding, our calculations provide evidence that concerns about the future impact of robots on the labor market have some basis in economic reality and thus merit further monitoring and analysis.
Appendix
Impact of Robots and Immigration on Native Employment, 2004–2016
FOOTNOTES
↵1. In January 2018, Erin Winick (2018) reviewed more than a dozen projections of the impact of technology on employment, nearly all which focused on occupations as the unit of study.
↵2. We can also use the supply-demand framework in figure 1 to model the influx of robots or immigrants as an inward shift in the demand for existing workers by Z efficiency units, with equivalent impacts on wages and employment.
↵3. The IFR also has a separate data set on the number of service-sector robots (World Robotics Service Robots) which shows that number to be growing rapidly (https://ifr.org/ifr-press-releases/news/why-service-robots-are-booming-worldwide, accessed June 27, 2019). But these data are limited over time and lack enough sectoral detail to be added to our current database.
↵4. Reprogrammable means a machine whose motions or functions can be changed without physical alteration. Multipurpose means a machine that can be applied to different applications. Physical alteration is alteration of the mechanical system as opposed to storage media, ROMs, and so on. Axis direction specifies the robot motion in a linear or rotary mode.
↵6. Indeed, expenditures on robots are included in surveys that ask for spending on plant and equipment as part of equipment. What differentiates robots from other plant and equipment is that robots are assumed to be more substitutable for human labor than other forms of capital. This assumption is the starting point for analyzing their impact on employment and wages separately from other inanimate factors of production.
↵8. Ilaski Barañano and Diego Romero-Ávila (2015) provide some macroeconomic evidence of a positive relation between growth and depreciation. John Fisher and Robert Pry (1971) developed a model in which technological change obsolesces older capital.
↵9. The U.S. Census Bureau (2017) developed a set of experimental questions on robots in its 2017 Census of Manufacturing that could be used to apportion robots within an industry by geographic location but the results are not yet publicly available.
↵10. The matching uses the industry variable in the Integrated Public Use Microdata Series (IPUMS) version of the ACS, IND1990, which reports a worker’s industry of employment based on the 1990 Census Bureau industrial classification scheme.
↵11. Because the annual file of the ACS is obtained from a series of monthly samples, the number of immigrants in survey year t who report arriving in that calendar year does not correctly estimate the total number of immigrants who arrived in that calendar year.
↵12. In particular, a worker’s sampling weight is multiplied by the fraction of the year that the person worked (defined as annual hours of work divided by two thousand). The ACS reports only the number of weeks worked for a small number of bracketed categories. Our calculation of the hourly earnings assigns a value of 7.4 to those who report working between one and thirteen weeks, 21.3 to those who report fourteen to twenty-six weeks, 33.1 to those who report working twenty-seven to thirty-nine weeks, 42.4 to those who report forty to forty-seven weeks, 48.2 to those who report forty-eight to forty-nine weeks, and 51.9 to those who report fifty-one to fifty-two weeks.
↵13. This removes persons with less than $2.60 and those with more than $154.70, in 2016 dollars.
↵14. We also estimated all regressions including the residual industry and the results were similar to those reported.
↵15. We also estimated regression models that include two-way interactions between industry and state, as well as between state and year. These models, however, tend to saturate the information in the data because we have no state variation in our measure of robot intensity and have much less time variation in the size of the immigrant supply shock in the post-2004 ACS data than in the immigration studies that use information spanning several decades beginning in 1960 and that thus compare periods of high immigration with periods of low immigration. Despite these data issues, the inclusion of two-way interactions leads to estimates for the robot effect that resemble those reported here.
↵16. Division bias is possible because the denominator of the robot and immigrant intensity variables gives employment in the industry-year cell (for the robot intensity variable) or in the industry-state-year cell (for the immigrant intensity variable). To avoid the bias, we redefined the two regressors by using the average level of employment in the industry or in the state-industry cell in 2001 through 2003 prior to the sample in estimating the regressions.
↵17. A firm will substitute a robot for a worker whenever the unit cost of having the robot do the work falls below the unit cost of the worker doing it, which will depend on the wage and the cost of the robot as well as their relative productivity. Technological change that produces more effective robots at a given cost or lowers the price of robots will induce firms to shift to robots unless wages fall commensurately. Robotworx estimates the cost of a robot: “Complete with controllers and teach pendants, new industrial robotics cost from $50,000 to $80,000. Once application-specific peripherals are added, the robot system costs anywhere from $100,000 to $150,000” (https://www.robots.com/faq/how-much-do-industrial-robots-cost, accessed June 27, 2019). If it costs $50,000 per year to run a system, including depreciation, the robot cost would rise to $150,000 to $200,000. At the average U.S. wage and salary of about $50,000, and benefits raising labor costs by 50 percent, the average worker costs the firm about $75,000. If the robot replaces two people, the robot would pay off in less than two years. Hence, the exponential growth of robots.
↵18. In 2017, about half of world exports in robots came from Japan (36.6 percent of total industrial robot exports) and Germany (14.2 percent). The United States was in fifth place (5 percent of exports), behind Italy and France (Daniel Workman, “Top Industrial Robots Exporters,” WTEx, June 4, 2019, http://www.worldstopexports.com/top-industrial-robots-exporters, accessed June 27, 2019).
↵19. More than half of robot sales in the United States are imports, Germany, Japan, and Switzerland being major sources of industrial robots (ExportUSA, “Sell and Export Industrial Robots in the United States: Industrial Automation Robotics in America,” June 10, 2017, https://www.exportusa.eu/export-industrial-robots-unitedstates.php, accessed June 27, 2019).
↵20. The first-stage regressions show that the robot intensity measure in the United States is strongly predicted by the robot stocks in Japan and Germany, and that the number of immigrant workers in each state-industry cell in the ACS is strongly predicted by the presence of immigrants in those cells in the 1970 Census.
↵21. O*NET contains on the order of one hundred measures of the skills and knowledge required in every occupation; the abilities, interests, and values needed to perform the work; the training and level of licensing and experience needed for the work; the work activities; and the physical, social, and organizational factors involved in the work (https://www.onetonline.org, accessed June 27, 2019).
↵22. We took the index for occupations on O*NET and transformed them into the OCC1990 occupation code available in the ACS available at IPUMS.
↵23. We also examined the relation between two other variables that some analysts view as indicating the likelihood of an occupation being prone to automation by robots and other technology—the routineness of cognitive work and the routineness of manual work (Autor, Levy, and Murnane 2003). These measures were largely independent of the automation variable and did not differentiate the effect of robots well.
↵24. The estimated coefficients reported in Acemoglu and Restropo (2017, table 3) for private-sector employment vary between –0.60 and –1.4 and for hourly wages between –1.5 and –2.5. Just as we report greater effects on earnings than on employment, their calculations show similarly larger impacts on earnings in most comparisons.
- © 2019 Russell Sage Foundation. Borjas, George J., and Richard B. Freeman. 2019. “From Immigrants to Robots: The Changing Locus of Substitutes for Workers.” RSF: The Russell Sage Foundation Journal of the Social Sciences 5(5): 22–42. DOI: 10.7758/RSF.2019.5.5.02. This work is part of the NBER Science and Engineering Workforce Projects (SEWP), and was supported by the NBER Sloan Foundation Grant, the Job Market for Older Workers as Retirement Recedes and Robots Do More Work (OWRR) (NBER G-2017-9943); the Harvard-IBM AI Automation On Labor (AIA-L) Research Collaboration Grant (Harvard 7643026-01-1-1); and the Century Foundation (for purchase of the IFR Robot Data). Direct correspondence to: George J. Borjas at gborjas{at}harvard.edu, Harvard Kennedy School, 79 JFK St., Cambridge, MA 02138; and Richard B. Freeman at freeman{at}nber.org, National Bureau of Economic Research, 1050 Massachusetts Ave., 3rd floor, Cambridge, MA 02138.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.