Abstract
Scholars continue to debate whether gains on the state tests used for accountability generalize to other measures of student achievement. Using panel data on students from a large urban school district, we estimate the impact of accountability pressure related to the No Child Left Behind Act on two measures of academic achievement: the state test and an “audit” test that is not tied to the accountability system. Overall, we find that accountability pressure is associated with increased state test scores in math and lower audit math and reading test scores. However, the sources of state and audit test score divergence varied by students’ race. Black students in schools facing the most accountability pressure made no gains on state tests, and their losses on audit math tests were twice as large as those of Hispanic students. These findings highlight the importance of better understanding the mechanisms that produce heterogeneous effects of accountability pressure across achievement measures and subgroups.
How do we know whether students are learning? At the time of the 1964 Civil Rights Act, the prevailing view on assessing educational opportunity was to measure the inputs of schooling, such as teacher qualifications and the presence of science laboratories in predominantly minority schools. Coleman’s Equality of Educational Opportunity report, required by section 402 of the Civil Rights Act, examined differences in inputs, but in a first for a national evaluation, it also examined differences in performance on standardized achievement tests. By shifting the discussion about equity from inputs to outputs, the EEO report transformed policy debates about the meaning of educational opportunity. For better or worse, in the years following the publication of the EEO Report scholars and policymakers came to define school quality in terms of standardized test scores. Culminating in the passage of the No Child Left Behind Act (NCLB), federal accountability relied heavily on standardized test scores, and teacher evaluations were increasingly tied to these scores as well.
With the newest reauthorization of the Elementary and Secondary Education Act—termed the Every Student Succeeds Act (ESSA)—authority over school-based accountability and teacher evaluation has devolved to the states, but the heavy reliance on standardized tests remains. Researchers have used state test scores to evaluate a wide range of policies, including high-stakes school accountability, charter schools’ effectiveness, and teacher merit pay. Policymakers also have called on these scores to make claims about changes in American students’ achievement over time, as well as changes in achievement gaps between historically advantaged and disadvantaged groups. Because state test score gains have not always been reflected in gains on other tests, such as the National Assessment of Educational Progress (NAEP) or international assessments, others have suggested that state test score gains in the NCLB era may be illusory (Koretz 2008).
Given substantial increases in accountability pressure in the last decade, there is renewed scholarly (Koretz 2013; Neal 2013) and media interest in understanding why state test score gains may not generalize to other assessments. At least three reasons that do not reflect changes in teachers’ instructional practice have been offered for the divergence between state test scores and audit test (those that are not directly tied to accountability) scores. The first is measurement error. In any given year, if a dog is barking outside of the classroom during a test, students may not perform up to their “true ability” on the test. However, we would not expect a measurement error–based mechanism such as this one to consistently favor state test performance, since random errors of measurement are equally likely to affect both types of test. Second, the timing of tests may differ, and that difference alone could lead to disparities in performance across tests. For example, if student growth curves on two tests are not parallel, or if test gains from one test depreciate over the summer more quickly than test gains from another, we might expect students to perform differently on tests given at the beginning of the school year compared to those given at the end of the school year. In addition, if differential rates of growth and depreciation vary by test and by student group (for example, lower-versus higher-income students), test timing may matter more for some groups than others. Third, students may not exert equal effort across all tests. For example, if a school holds a pep rally for the state test, students may try harder on that test than on other assessments.
The next three reasons for divergence may reflect accountability-induced changes in educational practice that are important in assessing the meaning of state test gains. The first of these is alignment between the domains to which the two tests intend to generalize. If these domains differ, we would not expect gains on state tests to generalize, and students in schools more “aligned” with state tests are likely to perform better on those tests. There is a fine line between alignment, however, and the second mechanism, which we describe as “teaching to the test.”
For our purposes, “teaching to the test” refers to activities intended to increase test scores more than students’ learning of the material has increased. This practice can raise scores because tests are based on a sampling principle, so that only a fraction of the domain is tested in any given year. Coaching students on material that predictably appears on the state test or presenting content in formats that mirror the state test are two of the most common forms of teaching to the test. State tests do not randomly sample from the state standards each year, so alignment to the state standards (“teaching to the standards”) may produce different instructional practices than alignment to the specific frequency with which standards predictably appear on state tests (“teaching to the test”).
Multiple factors have facilitated this type of teaching to the test. Test preparation firms have analyzed item maps from state tests to create benchmark tests and other materials that focus on predictably assessed standards. Teachers themselves can also access item maps linked to standards on many state education department websites. Recent studies provide suggestive evidence that teachers are responsive to test predictability: in a study of three states during the NCLB era (Jennings and Bearak 2014), students made larger gains on items testing predictable standards than on novel items. This finding could result from teaching to the test as opposed to teaching to the standards. If standards heavily sampled on the state test are not sampled at the same rate on an audit test, we would expect students to make larger gains on the state test.
Whether focusing on predictable content is a desirable practice depends on the relevance of each standard to the inference one wants to make from state test scores. State policymakers may believe that some standards are more important than others and explicitly build such guidance into their instructions to test designers. However, we are aware of no states that provided guidance to test firms at the individual standard level during the NCLB era; ultimately, testing contractors have made these decisions. If state tests are not designed with specific inference weights in mind for each standard, state test results may overstate learning and diverge from other test results when a small fraction of state standards are predictably tested over time and teachers focus their instruction on these standards.
Finally, heightened incentives to cheat on the state test may lead educators to alter student responses on the state test and not on other tests. One study that estimated the prevalance of cheating in the pre-NCLB era found that a minimum of 4 to 5 percent of Chicago Public Schools elementary teachers had cheated (Jacob and Levitt 2003). The prevalance of cheating in the NCLB era is unknown, but multiple cities have experienced cheating scandals in recent years. Some, like the scandal in Atlanta, have involved a significant number of administrators and teachers (Aviv 2014).
Despite the ongoing public debate about the meaning of state test score gains, no study has examined the impact of accountability pressure from NCLB on multiple tests taken by the same students. Our study addresses two research questions and, in doing so, informs policy debates about the effects of schools’ responses to external pressures on achievement and inequality and the possible heterogeneous effects of accountability policy across schools and student groups. First, we investigate the average effects of accountability pressure from failing to meet NCLB’s adequate yearly progress (AYP) targets for performance on both state tests and a second test, the Stanford Achievement Test, which we refer to as an “audit test.” We are interested in the direction and magnitude of these effects on both tests, as well as in whether accountability pressure is associated with an increased performance gap between the two tests. Second, we establish whether the effects of accountability pressure on the two tests differ across schools facing varying risks for failing to reach AYP targets. In both cases, we also ask whether accountability pressure increases the performance gap between the two tests for some types of students and schools more than others.
LITERATURE REVIEW
In what follows, we review the literature in two areas: the effects of accountability pressure on multiple measures of student learning and subgroups, and heterogeneity in responses to accountability pressure across schools.
The Effects of Accountability Pressure on Multiple Measures of Student Learning
A number of studies have found that accountability systems improve average student outcomes on both state and national tests (Carnoy and Loeb 2002; Dee and Jacob 2009; Hanushek and Raymond 2004; Jacob 2005, 2007; Rouse et al. 2007; Lauen and Gaddis 2012). We would not expect state test gains and state NAEP gains to perfectly track each other, but state test gains typically outpace state NAEP gains, and the magnitudes of these differences are large. Most recently, Brian Jacob (2007) has found that state scores grew twice as much as NAEP scores in Texas, North Carolina, Arkansas, and Connecticut. Studies conducted in the pre-NCLB era established similar patterns. For example, Daniel Koretz and Sheila Barron (1998) found gains in math scores on Kentucky’s state test three to four times as large as on the NAEP. Steven Klein and his colleagues (2000) found not only a similar pattern in Texas but also greater score inflation for black students than for white students. This research raises important questions about whether accountability pressure increases student learning more generally.
On the other hand, three national studies have found positive effects of No Child Left Behind on measures of student achievement beyond state test scores. These studies are distinctive from those just reviewed in that they use econometric approaches to establish NCLB effects; previous studies have looked at differential trends on two tests. The magnitude of these effects, however, is substantially smaller than the gains found on state tests. Thomas Dee and Brian Jacob’s (2009) study of the effects of NCLB on NAEP scores relies on a comparison of states that implemented accountability systems prior to NCLB with those that did not. They find that NCLB increased state NAEP scores in fourth- and eighth-grade math, but not in fourth- or eighth-grade reading. A strategy similar to Dee and Jacob’s is used in a related study by Manyee Wong, Thomas Cook, and Peter Steiner (2009), but they add to the analysis the level of difficulty of proficiency in each state; their results largely confirm Dee and Jacob’s. Wong and her colleagues find positive effects on fourth- and eighth-grade math scores and evidence of positive effects on fourth-grade reading scores when states also had high standards for proficiency. Randall Reback, Jonah Rockoff, and Heather Schwartz’s (2011) national study of schools in the Early Childhood Longitudinal Study: Kindergarten (ECLS-K) cohort finds small positive effects of NCLB accountability pressure on ECLS-K reading and science assessment scores, but no significant effects on ECLS-K math scores.
Our assessment of the importance of the generalizability of state test score gains to other measures of student achievement may also be affected if generalizability varied across student groups. For example, if gains for white students generalized from the state test to other exams but those for black students did not, we would want to assess further the instructional practices producing these results and consider whether differential exposure to particular instructional practices raises equity concerns.
Three previous studies of NAEP performance have examined the heterogeneous treatment effects of accountability systems but have focused only on their effects on one test—the NAEP. While Martin Carnoy and Susanna Loeb (2002) argue that strong accountability systems could narrow achievement gaps, Eric Hanushek and Margaret Raymond (2004) find that, relative to whites, Hispanics gained more in accountability states and black students gained less, though both of these point estimates fell short of statistical significance. Thus, the black-white achievement gap has actually increased as a result of accountability. More recently, as noted earlier, Dee and Jacob (2009) have estimated the impact of the No Child Left Behind Act by race and found decidedly mixed results across grades and subjects. For example, they identify larger positive effects for black and Hispanic students than for white students in fourth-grade math, but in fourth-grade reading white students gained while black and Hispanic students did not.
Taken together, these studies paint a mixed picture of the ability of accountability systems to narrow racial achievement gaps. Largely consistent across studies is the larger benefit for Hispanic students relative to black and white students, and the null effects of accountability on black students with the exception of fourth-grade math. Still, little is known about the effects of accountability pressure across demographic groups on multiple measures of student learning; addressing this gap is one goal of our study.
In sum, all of the studies described here establish positive average effects of NCLB beyond state tests but do not assess the generalizability of state test gains to other measures of achievement. Our study contributes to a small but growing literature examining the relationship between school-based responses to accountability pressure and student performance on multiple measures of learning, which requires student-level data and test scores from multiple exams. Only one study has examined the effect of accountability pressure on multiple tests, but this study is from the pre-NCLB era. Jacob (2005) used item-level data to better understand the mechanisms underlying differential gains across tests. Analyzing data from the Chicago Public Schools Iowa Test of Basic Skills (ITBS)—which at that time was high-stakes and used for student promotion decisions as well as school accountability—and a second measure of achievement, the Illinois Goals Assessment Program (IGAP), he found large gains on the high-stakes ITBS following the introduction of accountability, but no similar effects of the accountability system on the IGAP. Our study builds on those reviewed here by examining the effects of NCLB accountability pressure on schools in a district with multiple exams.
In the next section, we examine not only the average effects of accountability but the heterogeneous effects of accountability pressure across schools facing varying risks of failing AYP targets.
Heterogeneity in Responses to Accountability Pressure Across Schools
While the studies reviewed here have established the effects of accountability systems on outcomes, they have devoted less attention to studying heterogeneity in how educators perceive external pressures and react to them. Because the lever for change in accountability systems is educational improvement in response to external pressure, this is an important oversight.
The dominant view of educators’ responses to accountability incentives predicts that in the absence of accountability systems, “schools choose an allocation [of resources] based on preferences about the relative importance of helping students improve different types of skills and the relative importance of helping different types of students make improvements” (Reback et al. 2011, 3). NCLB, in this view, introduces costs and benefits that are a function of the fraction of students passing state tests. High-performing schools gain no benefit from resource reallocation if they are almost certain to make AYP targets with current practices. Low-performing schools, on the other hand, reap the benefit of meeting the AYP target, assuming resource reallocation is successful, but such reallocation may be excessively costly for schools that face little chance of making that target. The cost-benefit ratio is therefore likely to be largest for schools near, but below, passing thresholds, and smaller for schools well below or well above passing thresholds.
From this perspective, educators calculate how close they are to making AYP targets and are most likely to respond if their calculations place their school on the margin of making those targets. This is the extant view on schools’ responses to incentives in most of the economic and policy literature, which has documented a wide range of ways in which educators respond to accountability pressure by gaming the system (Figlio and Getzler 2002; Jacob 2005; Jacob and Levitt 2003; Neal and Schanzenbach 2010; Reback 2008). To be sure, work in this tradition acknowledges that schools with a low probability of making their AYP targets also face pressure to improve over a longer time frame. But these scholars generally contend that marginal schools will be the most responsive in the short term.
Other empirical evidence, however, is not consistent with this perspective. Combining school-level data on test performance and survey data from the RAND study of the implementation of NCLB in three states (Pennsylvania, Georgia, and California), Reback, Rockoff, and Schwartz (2011) find that the schools furthest from AYP targets were more likely to focus on students close to proficiency relative to those close to making AYP targets (53 percent of teachers versus 41 percent), to focus on topics emphasized on the state test (84 percent versus 81 percent), and to “look for particular styles and formats of problems in the state test and emphasize them in [their] instruction” (100 percent versus 80 percent). Another study reports larger effects of accountability pressure for the lowest-achieving schools than for schools near the margin of meeting proficiency targets (Jennings and Sohn 2014). Ethnographic and qualitative studies also suggest that schools with little chance of making the required targets nonetheless make substantial changes to their practice (Booher-Jennings 2005).
Our paper helps to adjudicate between these perspectives by contrasting modeling strategies that reflect these two theories of action. Determining whether schools on the margin of passing AYP targets are more responsive than those further away from doing so is important because it helps inform a theoretical understanding of schools’ responses to external pressure, as well as to shape the design of accountability systems.
DATA AND METHODS
We analyze a longitudinal administrative data set of sixth- through eighth-grade students tested in the Houston Independent School District (HISD) between 2003 and 2007. HISD is the seventh-largest school district in the country and the largest in the state of Texas. Our sample is 58 percent Hispanic, 29 percent black, 9.5 percent white, and 3 percent Asian. About 80 percent of students in our sample are considered by the state to be economically disadvantaged, which is defined based on free and reduced-price lunch and welfare eligibility.
A unique feature of this study is the availability of multiple test scores for each student—both the Texas Assessment of Knowledge and Skills (TAKS) and the Stanford Achievement Test battery. The TAKS is administered to students in grades 3 to 11 in reading and English language arts, mathematics, writing, science, and social studies; reading and math are the only subjects tested every year between grades 3 and 8. The Stanford Achievement Test is administered to all students in grades 1 to 11 in reading, math, language, science, and social science. In 1996, HISD added the Stanford Achievement Test under pressure from a business task force that sought a nationally normed benchmark test (McAdams 2000). In this respect, the Stanford was intended to serve as an additional audit on state tests scores. Since that time, all students except for those with severe disabilities have been required to take the Stanford. The TAKS and the Stanford have similar test administration features: both have flexible time limits, and all of these tests are given in the spring, from early March (Stanford) to mid to late April (TAKS).
For several reasons, the TAKS represents the district’s “high-stakes” test. First, and most important for our study, TAKS test scores are used to compute AYP under NCLB. Second, passing rates on these tests have been an integral part of Texas’s accountability system since 1994 (Reback 2008). Under this system—which served as the model for No Child Left Behind—schools and districts are labeled “exemplary,” “recognized,” “acceptable,” or “low-performing” based on their proficiency rates in each subject area. In most years, monetary rewards have been available for high-performing or improving schools, while low-performers are subject to sanctions, including school closure or reconstitution. Second, HISD has operated a performance pay plan since 2000 that provides monetary rewards to schools and teachers for state test results. Historically, the district based these rewards on campus accountability ratings, but in recent years it has rewarded individual teachers and schools based on their value-added on state tests. Third, during our study period, Texas required third-grade students to pass the TAKS reading test for grade promotion beginning in 2003. From 2005, fifth-grade students have been required to pass both the math and reading TAKS to be promoted.
The Stanford can be considered HISD’s “audit” test in that it is not tied to the state accountability system. However, this test plays several important roles in the district. For example, it is used as one criterion for grade promotion in grades 1 through 8. HISD students are expected to perform above a minimum standard on the Stanford (for example, one grade level below average or above) as well as on the TAKS. While the Stanford is not a binding standard, as it is in districts and states with strict promotion policies, HISD’s policy does provide an incentive for students to exert effort on the Stanford. In addition, the Stanford is used to place students in gifted, special education, and other programs. Finally, value-added measures from the Stanford tests have been a component of HISD’s teacher performance pay plan since 2007, the final year of our study. In sum, the Stanford is lower stakes for adults relative to the TAKS, but not so for students. For our purposes, it is ideal that students have good reason to exert effort on both tests, but that the significance of the state and audit tests for educators varies.
It is worth noting other similarities and differences between these tests beyond their uses in the school district. Both tests are untimed and multiple-choice. The TAKS is intended to be a test of the Texas state standards, which enumerate what students should know and be able to do. For example, the eighth-grade math test asks students to master thirty-eight standards in five areas of mathematics (algebra, geometry, measurement, numbers and operations, and statistics and probability). Our analyses of item-level data from Texas that link each item to a state standard show that just half of these standards make up 65 percent of the test points—more than enough to pass the test.
The Stanford, on the other hand, is intended to provide a broader portrait of students’ mastery in mathematics. Because the test is proprietary, we could not examine each item to assess content and complexity, but the test is aligned with National Council of Teachers of Mathematics standards. We have only been able to identify one analysis (Hoey, Campbell, and Perlman 2001) that maps the standards on the Texas Assessment of Academic Skills (TAAS) math test (in grade 4 only) to those covered on the Stanford; it finds considerable overlap, with 83 percent of the Texas standards represented on the Stanford. The Stanford is a bit more inclusive, with 74 percent of Stanford standards represented on the TAAS. Though we cannot quantify the breadth of the Stanford relative to the TAKS test, our analyses of item-level data from the TAKS suggest that predictable recurrences of certain standards may produce opportunities for teachers to focus more narrowly on tested content. The TAKS and Stanford tests are intended to test similar grade-level domains, but we do not argue that these domains are identical.
In sum, we believe that the Stanford is the best available instrument for assessing TAKS gains, but we recognize its limitations as well. Neither test has been validated against long-term outcomes. It is possible that gains on the TAKS do not transfer to the Stanford but nonetheless have important impacts on students’ long-term outcomes (Deming et al. 2013).
Our study focuses on the effects of accountability pressure, defined as failing to meet AYP targets, on the gap between the two tests for middle school students in HISD. We note that this is a conservative estimate of accountability pressure, as even schools with little risk of missing state accountability targets probably feel pressure to perform since test results are made public. We limit our analysis to middle school students because by 2005 sufficient numbers of middle schools had failed to meet AYP targets to permit variation on our independent variable of interest. (Such was not the case for elementary schools.) Relatively few middle schools failed to reach AYP targets in 2003 or 2004, so only 6 to 7 percent of middle school students were exposed to NCLB accountability pressure in the early years of our study (see table 1).1
Counts and Percentages of Students and Schools Failing to Meet AYP Targets, by Year
However, two changes in Texas education policy led to a large increase in schools failing to meet AYP targets over the period we study, and our analysis takes advantage of these policy changes. The cut scores for state tests were raised one standard error of measurement between 2003 and 2004 and again between 2005 and 2006. The percentage of students required to pass tests to make AYP standards also increased over this time: a nine- and six-percentage-point increase for math and reading, respectively, between 2004 and 2005, and another eight- and seven-percentage-point increase between 2006 and 2007. As a result of both the increase in cut scores and the level of performance required to make AYP targets, in 2006 and 2007 about one-third of students attended schools that faced pressure from NCLB to raise test scores, while very few students had faced such pressure in 2003.2 These policy changes allow us to provide a cleaner estimate of the effects of accountability pressure than would be the case in a setting in which standards for proficiency are constant. In that case, variation in exposure to accountability pressure would be driven more by year-to-year shocks in performance and related processes, such as mean reversion. In contrast, we can observe changes in test score performance both before and after schools are exposed to pressure to meet AYP targets.
One important additional feature of the TAKS tests that allows for analytical leverage is that the proficiency standard for reading is much less difficult relative to the distribution of student performance than the standard for math. In 2003, the base year of our study, 64.7 percent of sixth- to eighth-grade students were deemed proficient on the math test, while 84.1 percent were deemed proficient on the reading test. As a result, about 65.9 percent of school AYP failures between 2003 and 2007 were a function only of math performance, while approximately 19.5 percent were a function of both reading and math performance and another 14.6 percent were because of reading performance only. Although we lack the power in this study to formally test for the effects of these different types of failure, we predict that we will see more divergence between the math tests than between the reading tests when schools face accountability pressure.
There is also variation on failing to meet AYP targets among HISD high schools—given that some estimates place the high school dropout rate in HISD at about 50 percent (Swanson 2006)—but a high school estimation sample would be censored and greatly reduced in size. In 2005, for example, we had 13,991 ninth-graders; by 2007, we had only 8,569 eleventh-graders, a shortfall of about 39 percent. There appears to be some attrition from middle schools, but it is much lower than among high school students. In 2005, we had 11,854 sixth-graders; by 2007, we had 11,202 eighth-graders, a shortfall of about 6 percent.
We have also taken care to rule out the influence of other non-accountability shocks to the district during our study period. In the 2005–2006 school year, Houston schools enrolled more than 5,200 students (3 percent of that year’s student population) displaced by hurricanes Katrina and Rita. Two middle schools, Fondren and Revere, enrolled large numbers of displaced students. These schools failed to meet AYP targets owing to the performance of the special education subgroup, not that of the displaced students who had been exempted by the U.S. Department of Education from 2005–2006 AYP performance calculations.3 Nevertheless, the addition of hundreds of traumatized students to the already struggling middle schools in Houston probably had spillover effects that made it much harder for middle schools serving these students to meet AYP targets. That situation does not, however, affect our results, which, because we are examining the incentive effects of accountability threats on state and audit tests taken by the same students, are not sensitive to the exclusion of these schools from our sample.
We include all students enrolled in sixth through eighth grade between the years 2004 and 2007. We exclude students who took their TAKS test on a different campus than their Stanford test because of school mobility in the month between the two tests. Also excluded are those whose schools were exempted from AYP rating by NCLB (in 2003, four of forty-nine middle schools were exempted; in 2004 and 2005, two of fifty middle schools were exempted; and in 2006, two of forty-nine schools were exempted), schools with fewer than thirty students in any year, and schools with fewer than four panels. (In other words, we keep only schools with sufficient data on each year between 2004 and 2007, inclusive.) Our final repeated measures analysis sample includes about 74,000 unique students. Descriptive statistics on the sample of about 136,000 student-year observations are shown in table 2.
Descriptive Statistics
The primary dependent variable in our study is the gap between the state test (TAKS) and audit test (Stanford) scores, which have been standardized by grade level and year. However, beyond estimating the size of the gap, we are interested in how the gap arises. For example, a gap of 0.1 standard deviations could arise if students made progress on both tests, if they made progress on the state tests and not the audit tests, or if they fell back on both tests. We thus present models of the gap along with models separately predicting state test and audit test performance. The focal independent variable in our study is an indicator, coded [1,0], recording whether a school failed NCLB’s AYP target in the previous year. We posit that schools failing to reach the AYP target would be under pressure to increase test score achievement the following year.4 Whether teacher and principal actions focus on raising general academic skills or test-specific skills is the primary question of this study. Therefore, we hypothesize that students attending schools under accountability pressure from failing to reach AYP targets in the previous year will have larger test score gaps between the two tests than the same students had in years in which their schools met AYP targets in the previous year. In our view, this is because accountability pressure alters the relative costs and benefits of teaching state test–specific versus general academic skills content. As we discuss in detail later, whether teaching state test–specific skills is a positive or negative outcome is the subject of substantial debate.
Our primary specification is a regression with student fixed effects:
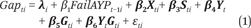
In brief, equation 1 predicts the state test–audit test score gap for student i at time t as a function of whether the student’s current school failed to meet AYP targets the previous year, controlling for student fixed effects, λi, student time-varying controls, Xit, school time varying controls, Sit, and year, grade, and year-by-grade fixed effects, Yt, Git, and YtGit, respectively. We hypothesize that net of controls, β1 will be positive because failure to meet accountability targets will cause teachers to focus more time and effort on state test–specific skills rather than on more general skills. We use a student fixed-effects model to control for students sorting into schools based on fixed unobservable student and family background characteristics. This approach eliminates all time-invariant between-student confounding and produces consistent parameter estimates when there is no within-student confounding of the accountability effect (that is, the accountability effect is uncorrelated with time-varying unmeasured student characteristics). The student fixed-effects approach requires within-student variation on accountability status to identify parameters. We identify the accountability effect from year-to-year variation in the accountability status of students’ schools. This status changes due to (a) students switching to schools that differ on accountability status, and (b) variations in the classification of students’ schools as they progress through grade levels in the same middle school. Following standard practice in longitudinal data analysis, our student fixed-effects models have cluster-correct standard errors to adjust for non-independence within students. (We have repeated observations within students over time.)
Schools’ Risk of Failing to Meet AYP Targets, 2004–2007
Student Fixed-Effects Models Predicting the Effect of Failing to Meet AYP Targets on Standardized Achievement Levels and Gaps in Levels
Student Fixed-Effects Models Predicting the Effect of Schools’ Risk of Failing to Meet AYP Targets on Standardized Achievement Levels and Gaps in Levels
As robustness checks, we present alternative specifications with school fixed effects and both student and school fixed effects. We also present random effects specifications. These alternative specifications, reported in tables 6 and 7, produce almost identical results. The school fixed-effects models in these tables have cluster-corrected standard errors to adjust for the non-independence of student observations within schools. Models including both student and school fixed effects have cluster-corrected standard errors to adjust for non-independence within student-school “spells.”5 In addition, in response to potential concerns that our findings could be driven by mean reversion, we replace the dependent variable with a gain measure that explicitly adjusts for the student’s position in the previous year’s test score distribution (Reback 2008). Results with this dependent variable (tables 6 and 7) are consistent with those with test score level as the dependent variable.
Comparison of Alternative Specifications of the Effect of Failing to Meet AYP Targets
Comparison of Alternative Specifications of the AYP Risk Effect
The student fixed-effects model shown in equation 1 assumes a homogeneous treatment effect of failing to meet the target, that is, that all schools below the metric’s threshold will experience the same incentives for improvement, and that all schools above the metric’s threshold will experience the same incentives for improvement. To relax this assumption, we also test a model that defines accountability pressure in terms of risk of failing AYP targets. As we discussed in the literature review, there are two competing perspectives about schools’ responses to accountability pressure. It could be that schools at the margin of passing AYP targets have the largest incentive to boost state test scores, while schools well above or well below that margin have weaker incentives to do so. On the other hand, qualitative work suggests that schools at high risk of missing targets are very responsive to accountability pressure (Hallett 2010) even when their odds of making targets are extremely low.
To test for heterogeneous effects by school risk of failing AYP targets, we first compute the year- and school-specific probability of failing as a function of school average and subgroup average test scores and compositional characteristics:
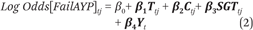
where T is a vector of school-level average test state and audit math and reading test scores along with squared and cubed terms of each, C is a vector of compositional characteristics (percentage black and percentage economically disadvantaged and squared and cubed terms of each), SGT is a vector of subgroup-specific average test scores (school-level subgroup test score averages for black, Hispanic, and economically disadvantaged students), and Y is a vector of year fixed effects. Using the predictions from equation 2, which correctly classifies 91 percent of the school-year observations, we define the following risk categories: low risk (0 to 0.35 probability of failing to meet AYP targets), medium risk (0.35 to 0.65), and high risk (0.65 to 1). Across all years, most schools fall into the low-risk category (81 percent), and about 9 to 10 percent fall into the medium- or high-risk categories (table 3).
The probability of failing to meet AYP targets, however, increases over time. For example, between 2004 and 2007, the percentage of middle schools in the low-risk category fell from 96 to 70 percent, and the percentage of schools in the high-risk category increased from 0 to 21 percent. We thus define indicator variables for high and low risk of failing to meet AYP targets and estimate that:
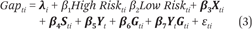
Negative coefficients on the High Risk and Low Risk variables would indicate that students in schools at the margin of passing AYP targets have larger gaps between the two tests than students in schools either well below or well above the margin. Because previous research suggests that the effects of accountability pressure differ for Hispanic and black students (Hanushek and Raymond 2004), we estimate models 1 and 3 separately for black, Hispanic, and economically disadvantaged students.
RESULTS
The results of student fixed-effects models based on equation 1 estimated on the state test–audit test gaps in each subject are shown in models 3 and 6 of table 4. Also shown in the table are models with the state and audit test scores as dependent variables. The first row displays estimates from all students in our analytic sample. The next three provide separate estimates for black, Hispanic, and economically disadvantaged students, respectively; we do not separately estimate regressions for white and Asian students because only a small fraction of these students were in schools facing accountability pressure. The all-student coefficient on the Failed AYP variable from model 1, 0.0374, indicates that students in schools in the year immediately following an accountability threat from NCLB have state math test scores that are about 4 percent of a standard deviation higher than students in schools that face no accountability threat from NCLB. The coefficient from model 2, −0.0232, from a regression with the audit math test as the outcome, indicates a significant negative test score difference between students in schools facing accountability threats relative to those in schools not facing such threats. The math gap, shown in model 3, is essentially the difference between columns 1 and 2. The coefficient, 0.0607, is positive and statistically distinguishable from zero, which suggests that the NCLB accountability threat has a larger effect on math state test scores than on audit math scores. Increases in the state test–audit test gap in math suggest that schools are responding to the incentives in NCLB to raise test scores on the assessment linked to the state standards and AYP calculations. In this case, these effects do not generalize to performance on the audit test; in fact, they produce a small decline in these scores.
In reading, the small and negative effects we find on both reading scores produce a null reading gap. This could have occurred for at least two reasons. First, many of the studies cited earlier have found larger effects of accountability pressure on math compared to reading. Second, the fraction of students in Houston failing mathematics tests was significantly higher than for reading, such that schools facing accountability pressure were more likely to have missed AYP targets because of their math scores and thus to have had an incentive to focus more heavily on math.
The conclusion that schools facing accountability threats tend to produce larger state test–audit test math gaps holds across black, Hispanic, and economically disadvantaged subgroups, which all have positive math gap effects. That is, we find that accountability pressure increases the gap in performance on the two tests. The point estimate for blacks is somewhat larger than for other groups, and the patterns across the state and audit tests differ. While the Hispanic gap between the two tests emerges because of gains on the state test and small losses on the audit test, black students experience no gains on the state test and a loss of 0.06 standard deviations on the audit test. We see this pattern emerge again for reading tests, where the effects on reading gaps between the state test and audit test are small, positive, and statistically significant for black students. This gap is produced by black students making no gains on the state test and experiencing losses on the audit test.
These effects may be conservative because they do not distinguish among the types of schools most at risk under NCLB. As noted earlier, we have defined “risk sets” of schools based on their probability of failing to meet AYP targets. Incentives-based perspectives predict that the effects of incentives to increase state test scores rather than audit test scores will be the strongest for schools at the margin of failing to meet AYP targets. This hypothesis predicts that (1) schools at very low risk of failing to meet AYP targets will have null or negative accountability-induced gaps (that is, their gains on the audit test will be larger than those on the state test) as these schools focus more on skills that are not test-specific, and (2) schools at the margin of failing to meet AYP targets will have large accountability-induced gaps and schools virtually certain of failing to meet AYP targets will have somewhat smaller accountability-induced gaps than schools at the margin of failing. On the other hand, schools well below the AYP threshold face the most severe sanctions in the medium to long term. This perspective predicts that schools virtually certain to fail to meet AYP targets will have the largest accountability-induced gaps, schools at the margin will have somewhat smaller gaps, and schools at low risk of failure will have no gap or negative gaps overall.
Table 5 presents the effects of accountability pressure defined as high and low risk of failing to meet AYP targets for all students and separate estimates for black, Hispanic, and economically disadvantaged students. If schools are only focused on short-term incentives, we would expect to see the greatest response by schools at medium risk of failing to meet AYP targets. The first coefficient in column 1 of table 5, 0.0418, indicates that for all students the high-risk–medium-risk difference in math state test scores is about 4 percent of a standard deviation. In other words, students in schools at high risk of failing to meet AYP targets have higher math state test scores in the subsequent year than students in schools at the margin of passing AYP targets. By contrast, students in schools at high risk have lower math audit test scores (−0.0585) in the subsequent year than students in schools at the margin. The accountability-induced state test–audit test gap is therefore 0.100 of a standard deviation, which indicates that relative to students in schools at the margin of passing AYP targets, students in schools at high risk of doing so have larger gaps. The high-risk–medium-risk differential in the reading gap is also positive, but smaller, at 0.0413. Turning to the low-risk–medium-risk differential, we find negative gap scores in math and no gap in reading. Students in low-risk schools gained on audit tests even as their state tests declined. We note that these results are not due to ceiling effects on the state tests.
Overall, the pattern of coefficients in table 5 suggests that when schools face additional pressure, they either become more aligned to state standards or “teach to the test.” We make this inference because high-risk schools see increases in state test scores and decreases in audit test scores in both subjects, while low-risk schools are more likely to make progress on the audit test. Our results alone cannot differentiate between these two mechanisms, but we believe that it is important to note that greater accountability pressure appears to produce specific versus general gains. We return to the normative questions raised by this finding in the discussion.
Moving to the subgroup results, the bottom panels of table 5 show that black, Hispanic, and economically disadvantaged students experience approximately the same accountability-induced state test–audit test gap in high- and low-risk schools in both subjects. However, the sources of the gap vary across subgroups, for the math test in particular. Based on our point estimates, black students in high-risk schools experience audit test losses approximately twice as large as those experienced by Hispanic students (0.108 standard deviations versus 0.043 standard deviations for Hispanics) and do not benefit on the state test. In contrast, Hispanic students gain 0.057 standard deviations on the state test. Although our data cannot explain why black students lose more than Hispanic students on the audit math tests, we note that the pattern of Hispanic students benefiting more from accountability pressure has been documented in other studies (Hanushek and Raymond 2004; Lauen and Gaddis 2012).
Sensitivity Analysis
Alternative Fixed- and Random-Effects Specifications
A student fixed-effects model removes observable and unobservable within-student confounding. We estimate two alternative specifications to determine whether our results are vulnerable to different kinds of confounding threats. Including school fixed effects removes between-school confounding. This model identifies the effect of failing to meet AYP targets on state test–audit test gaps on across-cohort variation within the same school over time. This model, presented in model 2 of table 6, produces almost identical effects on math and reading gaps as the student fixed-effects model. (Included in this table are results from all students in the analytic sample.) Including both student and school fixed effects in the same model identifies the effect of failing to meet AYP targets on gaps in within-school variation across time only for groups of students who remain in the same school (the “stayers”). This specification also produces very similar effects (model 3 of table 6). These alternative specifications do not alter our conclusions about the differences between high- and medium-risk schools (see table 7). The school fixed-effects models provide somewhat weaker evidence on differentials among the three risk categories, but the models with both student and school fixed effects, which adjust for both between-student and between-school confounding, reproduce the student fixed-effects results. In addition, when we estimate our models with random rather than fixed effects, the results (reported in column 4 of table 6) are similar.
Testing for Mean Reversion
Another concern is that our results could be driven by mean reversion. We have performed two additional analyses to address this threat. First, we have added additional test score lags to our model to help control for the possibility that students in schools failing to meet AYP targets had a one-year deflection from their “true” score and led the school to fail. Second, we have estimated additional models with an “adjusted gain” measure as the dependent variable to account for the possibility that one-year differences signify larger or smaller gains at different points in the prior-year achievement distribution. Following Reback (2008), for each subject we define a standardized adjusted gain score as the difference between the actual test score of a student (i in equation 4) in year t and the expected score for students in the same grade (g) who had the exact same score as in the previous year, normalized by the standard deviation of the scores in year t for that group of students (that is, the same grade and score in the previous year):
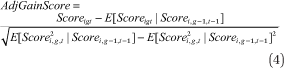
Our results are robust to both of these alternative specifications. For example, the all-student estimate in math shown in table 4 is 0.0607 (0.0065), p < 0.001. The same estimate with one- and two-year lags in both reading and math (four total) is 0.0506 (0.0088), p < 0.001. As shown in table 6, the estimate from a model with adjusted gain in math as the dependent variable is 0.0911 (0.0181), p < 0.001.
DISCUSSION
To summarize our results, we find that accountability pressure from the No Child Left Behind Act is associated with increased scores on math state tests, but lower math and reading scores on audit tests. The state test–audit test gap is largest for math, and the fact that two-thirds of schools in our study missed AYP targets because of the math test helps to contextualize this finding; we would expect to see more divergence on the math test than on the reading test.
We believe that our study provides the best available evidence about the effects of accountability pressure on multiple tests in the NCLB era, since we are able to measure the performance of the same students on two different tests and compare their own performances in years when their schools faced different levels of accountability pressure. For students in schools most at risk of failing to meet AYP targets, the gap between the gains in math state test scores and losses in math audit test scores is a nontrivial 0.10 standard deviations; the gap for reading is 0.04 standard deviations. To benchmark the size of these effects, the math effects are approximately the same size as the estimated effects of accountability in a recent National Research Council (NRC) report, which estimates the effects at 0.08 standard deviations (Elliott and Hout 2011). We also find that the sources of state test–audit test gaps vary across student groups. Most importantly, black students in higher-risk schools do not experience gains on the state reading and math tests, but experience losses twice as large as Hispanics do on the audit math test.
In addition to identifying these average effects, our findings on heterogeneous responses across schools help to revise the current “rational choice,” incentives-based approach to understanding educators’ responses to external pressures. Our results demonstrating that schools well below AYP targets have larger state test increases than schools at the margin of those targets raise doubts that educators are driven primarily by short-term, “rational” responses to incentives and show that the lowest-performing schools are indeed responsive to pressure, even when they have little chance of making the target. That increases on state tests do not generalize to audit tests, however, indicates that educators are also driven by short-term incentives to raise test scores on the state test. This mix of findings suggests that educators in this era of accountability are best understood as driven by both short- and longer-term imperatives.
In this discussion, we evaluate our findings in light of the most likely mechanisms for divergence across tests that we outlined at the outset of the paper. Understanding these mechanisms is important for evaluating their implications for equality of educational opportunity. One possibility is that effort alone explains differences between state test and audit test performance in schools failing to meet AYP targets. It is useful to make clear the conditions that are necessary for differential effort to explain these effects. Recall that any time-invariant component of lower motivation on the audit test (the possibility that students always try harder on the state test and less hard on the audit test) is removed in our specifications because of our use of student fixed effects. For student effort to explain our results, students would have to exert less effort on the audit test in years when their schools face pressure relative to their own effort when their schools do not face pressure. This could occur, for example, if teachers in these schools explicitly or implicitly tell students, or students conclude on their own, that the audit test is not worthy of the same effort in years when their schools face pressure and that the state test deserves additional effort. To explain our math findings, both of these conditions must be met. Second, we note that the audit tests are given in each year approximately a month before the state tests, which makes “test fatigue” less likely as an explanation for worse audit test performance. We do not believe that the pattern of results presented in this paper provides strong support for the effort explanation, but we note that our study cannot definitively rule out this possibility.
A second possibility is that when schools face accountability pressure, educators increase their alignment with state standards. If state tests are aligned with state standards, better instructional alignment alone should produce an increase in state test scores. Increased alignment may also reduce the coverage of topics that are tested on the audit test. If the skills represented in the state test are sufficiently narrow, alignment would tend either to leave audit scores unchanged or to decrease those scores if other material has been supplanted.
Whether increases in state scores at the expense of audit scores is a positive outcome depends on one’s understanding of alignment. In the current testing debate, one person’s “alignment” is another person’s “teaching to the test.” One perspective on alignment holds that if standards represent skills that we want students to learn and tests are aligned with these standards, alignment-based increases in scores are a positive outcome and declines in performance on tests less aligned with these standards are of little importance.
Another perspective suggests that alignment-based increases should be evaluated more critically. According to Koretz (2005, 112), because of the sampling principle of testing, “alignment of instruction with the test is likely to produce incomplete alignment of instruction with the standards, even if the test is aligned with the standards. . . . Despite its benefits, alignment is not a guarantee of validity under high-stakes conditions.” In theory, the issues raised by Koretz could be addressed if we are willing to fully articulate the domain of skills that we care about and to devote unlimited testing time and resources toward fully sampling the domain and a variety of representations of these skills. The experience of testing under No Child Left Behind, however, has been that tests have not been aligned with state standards, and state tests have often predictably sampled a small number of standards that are not a priori the “most important” (Holcombe, Jennings, and Koretz 2013).
As with any quantitative analysis using only administrative data, we cannot determine the mechanisms that produce state test gains that do not generalize to the audit tests, but we believe that we have presented compelling evidence here to encourage future scholars to investigate how instruction changes when schools face accountability pressure, why gains vary across different measures of achievement, and why gains vary across different subgroups of students.
Acknowledgments
We thank Peter Crosta, Kari Kozlowski, Casey Megan, and Heeju Sohn for their research assistance and Karl Alexander and Steve Morgan for their helpful comments.
FOOTNOTES
↵1. We have “forward-lagged” school accountability status, so schools failing to meet AYP targets in 2003 appear in table 1 as failing in 2004. Accountability ratings appear over the summer following spring testing. Therefore, the following year’s AYP status could affect school practices and student test scores only in the following year.
↵2. An ideal analysis would not only examine the effects of overall AYP status but estimate the effects of subgroup-specific failure. In our study, only half of the schools that failed to reach AYP targets did not also miss the “all students” AYP target, so we lack the power to estimate these impacts on individual subgroups. By estimating the effect of AYP failure on all students, our analysis may miss responses at the subgroup level. This makes it more likely that the AYP effects reported here are lower bounds of the true effect (that is, that they are conservative estimates).
↵3. Statistics and background related to students displaced by hurricanes Katrina and Rita come from letters from the Texas Education Agency and the U.S. Department of Education dated August 1, 2006, and August 8, 2006, respectively (available from authors upon request). The results presented here include Revere, while sample restrictions exclude Fondren from our analysis sample. Excluding Revere from our analysis sample does not affect our findings (results from authors upon request).
↵4. As noted previously, schools may fail to meet AYP targets because they miss targets for one or more subgroups. In a large enough sample, we could model the impact of subgroup-specific failure on students’ academic progress. In our sample, however, approximately half of schools fail on the “all students” indicator as well as for subgroups; this limited sample does not allow us to investigate the role of subgroup failure. We note that our estimates should thus provide a conservative estimate of the impact of failing AYP on all students.
↵5. Spells are student panels that lie within the same school. A student who spends all three years in the same middle school has only one spell. A student who switches schools once has two spells in two different schools.
- Copyright © 2016 by Russell Sage Foundation. All rights reserved. Printed in the United States of America. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Reproduction by the United States Government in whole or in part is permitted for any purpose. We thank Peter Crosta, Kari Kozlowski, Casey Megan, and Heeju Sohn for their research assistance and Karl Alexander and Steve Morgan for their helpful comments. Direct correspondence to: Jennifer L. Jennings at jj73{at}nyu.edu, 295 Lafayette St., 4th Floor, New York, NY 10003; and Douglas Lee Lauen at dlauen{at}unc.edu, Department of Public Policy, UNC-Chapel Hill, Abernethy Hall, CB#3435, Room 121A, Chapel Hill, NC 27599.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.