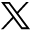Abstract
I use standardized test scores from roughly forty-five million students to describe the temporal structure of educational opportunity in more than eleven thousand school districts in the United States. Variation among school districts is considerable in both average third-grade scores and test score growth rates. The two measures are uncorrelated, indicating that the characteristics of communities that provide high levels of early childhood educational opportunity are not the same as those that provide high opportunities for growth from third to eighth grade. This suggests that the role of schools in shaping educational opportunity varies across school districts. Variation among districts in the two temporal opportunity dimensions implies that strategies to improve educational opportunity may need to target different age groups in different places.
Are public schools in the United States engines of mobility or agents of inequality? Can schools in low-income communities provide a pathway out of poverty, or are the constraints of poverty too great for schools to overcome? Such questions are at the heart of debates about the role of education in social mobility in the United States. Despite decades of research, however, we still lack clear answers.
In this article, I provide new evidence to inform these debates. It suggests that the lack of a clear answer to the question is explained in part by the substantial variation in the role of schooling in shaping educational opportunity across places. Early childhood conditions are more important in some places, educational opportunities during the elementary and middle school years more important in others.
The article also provides a demonstration of how administrative test score data can be used to construct high-resolution place- and age-based measures of educational outcomes, despite a number of major limitations of available administrative data. In particular, the standardized tests used in schools vary across place, grade, and year; the resulting scores are typically coarsened into a small number of ordinal categories whose definitions also vary across place, grade, and year; and the scores are reported only in repeated cross-sectional aggregate format rather than as student-level longitudinal records. Although these features of educational testing and reporting limit some potential uses of administrative test score data, the data can nonetheless provide useful information about the spatial and temporal structure of educational opportunity in the United States.
In this article, I first use standardized test scores from roughly forty-five million public school students tested during the school years 2008–2009 through 2014–2015 to construct measures of the temporal structure of educational opportunity in more than eleven thousand school districts—almost every district in the United States. By a school district, I mean the geographically defined community—including all of its local institutions—served by a public administrative school district. When I refer to the opportunities available in a district, I therefore mean the opportunities available to children living in that district, including the educational opportunities they have in their homes, neighborhoods, childcare and preschool programs, afterschool programs, and their public schools.
For each school district (read “community”), I construct two measures: the average academic performance of students in grade three and the within-cohort growth in test scores from grade three to eight. I argue that average test scores in a school district can be thought of as reflecting the average cumulative set of educational opportunities children in a community have had up to the time when they take a test.
Seen this way, the average scores in grade three can be thought of as measures of the average extent of “early educational opportunities” (reflecting opportunities from birth to age nine) available to children living in a school district. Research suggests that these early opportunities are strongly related to the average socioeconomic resources available in children’s families in the district. They may also depend on other characteristics of the community, including neighborhood conditions, the availability of high-quality childcare and preschool programs, and the quality of schools in grades K–3.
The growth in average test scores from grades three to eight can likewise be thought of as a measure of the average extent of middle childhood educational opportunities available to children living in a school district when they are roughly age nine to fourteen. Given the prominence of schooling in children’s lives at these ages, these opportunities may depend in large part on the quality of the local elementary and middle schools. They may also depend on average family resources, of course, as well as other local conditions, including neighborhood characteristics and the availability of afterschool programs.
Given these two measures, average scores in eighth grade are then understood to reflect the cumulative set of early and middle grade educational opportunities available to children in a school district. The decomposition of eighth grade average scores into the two components, reflecting early opportunity and middle grades opportunity, provides insight into the temporal structure of educational opportunity. The availability of these two measures for more than eleven thousand school districts yields unprecedented insight into the geographic and temporal structure of childhood educational opportunity in the United States.
In the second part of this essay, I describe both the relationship between these two measures and their association with socioeconomic characteristics of school districts. I find that the two measures are largely uncorrelated; early and middle grade opportunities appear to be distinct and separable dimensions of local educational opportunity structures. Among districts with a given level of average test scores in third grade, variation in growth in average scores from third to eighth grade is wide. Moreover, although both dimensions of opportunity are positively associated with district socioeconomic conditions, the correlation is much weaker for the middle grades growth dimension. Many low-income school districts have relatively high measures of growth and many affluent districts have relatively low growth. Finally, I also examine the temporal opportunity structure separately by racial-ethnic group and for poor and nonpoor students.
I conclude with two discussion sections. The first reflects on the value and limitations of the administrative data I use here, the process of obtaining the data and constructing the measures I use, and other potential uses of these data. The second reflects on the substantive patterns evident in the data, linking them to several scholarly and policy discussions. These patterns suggest that the role of schooling (and factors that shape children’s academic progress during the years they are in school) in shaping educational opportunity (and perhaps social mobility) varies across communities. The answer to the question of whether schools exacerbate or ameliorate socioeconomic inequality may be “it depends on where you live.” Moreover, the variation among districts in the two temporal opportunity dimensions implies that strategies to improve educational opportunity may need to target different age groups in different places. Finally, one implication of the low correlation between growth rates and average third-grade scores is that measures of average test scores are likely very poor measures of school quality. The growth measure I construct does not isolate the contribution of schools to children’s academic skills but is likely closer to a measure of school effectiveness than measures of average test scores are.
BACKGROUND
Educational outcomes vary widely by socioeconomic status and race-ethnicity in the United States. Children in high-income families, and those whose parent or parents have college degrees, systematically score higher on standardized tests and are more likely to attend and graduate from college than lower-income students and students whose parents did not attend college. Similar disparities are evident between white and Asian students and African American, Hispanic, and Native American students (Chetty et al. 2017; Reardon 2011; Reardon, Robinson-Cimpian, and Weathers 2015; Sirin 2005; Ziol-Guest and Lee 2016). This inequality in average group outcomes is prima facie evidence of systematic between-group differences in opportunity because average academic capacities do not differ among groups (Nisbett 2011; Nisbett et al. 2012; Nisbett 1998). But disparities in outcomes alone do not indicate the ways in which opportunities differ, nor the developmental stage when they are most salient. In particular, they do not tell us to what extent schools—and inequalities in schools—are to blame for these patterns. Here I briefly discuss two strands of scholarship that are relevant to this question: debates about the role of schools in shaping inequality, and evidence regarding place-based opportunity structures.
Schools as “the Great Equalizer” in the United States
The debate regarding schools’ role in providing educational opportunity and facilitating social mobility has a long history, particularly among sociologists. Three dominant arguments shape the debate. One position holds that schools reduce inequality of opportunity. The stark inequality in children’s family backgrounds creates large differences in children’s opportunities to learn, but school environments—in this argument—are less unequal than children’s home environments. Evidence for this view comes from research showing, for example, that racial or socioeconomic achievement gaps widen in the summer when children are not in school, but narrow (or at least do not grow) when children are in school (Alexander, Entwisle, and Olson 2001, 2007; Downey and Condron 2016; Downey, von Hippel, and Broh 2004; Entwisle and Alexander 1994). This evidence is sensitive to the scale used to measure academic performance, however: not all studies show these same patterns (von Hippel, Workman, and Downey 2017). Additional support for this argument comes from studies showing that poor children benefit more from expanded time in school—via universal preschool enrollment, universal kindergarten, full-day kindergarten, and extended school days—than nonpoor children (Raudenbush and Eschmann 2015).
A second position is that schools have relatively little effect on the inequality of educational outcomes; family background is a far stronger force than schooling. In this view, most educational inequality is produced early in children’s lives and by differences in family resources. This was the conclusion of the 1966 Coleman report, and was, to some extent, the argument of Christopher Jencks and his colleagues (Coleman et al. 1966; Jencks 1972). Additional evidence for this view comes from studies that find that socioeconomic or racial achievement gaps are large when children arrive in formal schooling in kindergarten, and do not change appreciably during the schooling years (Reardon 2011; Reardon, Robinson-Cimpian, and Weathers 2015).
Related to this argument is extensive evidence documenting the developmental importance of early childhood experiences. Family income when children are young is particularly consequential, relative to family income when children are older, for children’s educational development (Duncan and Brooks-Gunn 1997; Duncan, Brooks-Gunn, and Klebanov 1994). Early childhood interventions can have significant and lasting impacts on children’s outcomes (Duncan and Magnuson 2016; Heckman, Pinto, and Savelyev 2013). And, conditional on income, where one lives as a young child appears to have more effect on college attendance and income in young adulthood than where one lives as an adolescent (Chetty, Hendren, and Katz 2016). The salience of early childhood experiences may mean that experiences during middle childhood and adolescence are relatively unimportant in comparison.
Counter to this argument, however, are case studies and evaluations showing that schooling interventions or policies can have significant effects on achievement gaps, at least in some schools or as a result of specific interventions (Abdulkadiroglu et al. 2011; Bloom and Unterman 2012; Dobbie and Fryer 2011). Lottery-based studies of charter schools, likewise, reveal considerable heterogeneity in both charter and traditional public schools’ effectiveness (CREDO 2015; Tuttle, Gleason and Clark 2012). This implies that malleable features of schools can have sizeable effects on students’ academic performance.
The third view is that schools are powerful agents of inequality. In this view, not only can schools have sizeable effects on student achievement, but social policies and economic forces also conspire to ensure that schools in high-poverty neighborhoods are systematically inferior to those in affluent communities. In this view, schools exacerbate social inequalities, in large part because society systematically invests little in poor children’s schools. Evidence for this comes from studies showing that schools in low-income communities have less-qualified teachers (Boyd et al. 2005; Lankford, Loeb, and Wyckoff 2002) and weaker curricula (Darling-Hammond 1998). An older strain of research argues that high-poverty schools have systematically fewer financial resources (see, for example, Kozol 1967, 1991), though in many—but not all—states this is no longer true, at least in terms of average per-pupil financial resources (Chingos and Blagg 2017). An alternate, neo-Marxist version of this argument holds that capitalism requires an unequal schooling system to prepare students of different class background for their future roles in a capitalist economy (Bowles and Gintis 1976).
Each of these arguments has both supporting and countervailing evidence. This is both because there is some truth to each of them and because the role of schooling varies across place.
Geographic Variation in Educational Opportunity
Much of the discussion of the role of schools or the importance of early childhood is concerned primarily with the average patterns of educational opportunity available to different socioeconomic or demographic populations. But recent research demonstrates that educational opportunity also varies significantly by location, even conditional on family income. Children’s educational outcomes—test scores, high school graduation rates, and college enrollment and attendance rates—vary widely across the United States. Raj Chetty and his colleagues, using tax records of twelve million children born in the United States in the early 1980s, demonstrate that this variation is substantial, even conditional on family income (2014). Among children born to families at the 25th percentile of the income distribution, for example, college enrollment rates range from less than 25 percent to more than 65 percent across the 709 commuting zones they study.1 That is, educational opportunity is a function of both place and family resources.
This is consistent with research on neighborhood effects, which argues that neighborhood contexts play a role in shaping educational outcomes (Chetty, Hendren, and Katz 2016; Harding 2003; Sampson, Sharkey, and Raudenbush 2008; Wodtke, Harding, and Elwert 2011). Much of this literature, however, focuses on the effects of neighborhood economic conditions; research has been less successful at identifying the mechanisms through which neighborhood contexts and community institutions shape educational opportunity. Chetty and his colleagues note that upward economic mobility of children born to low-income families is lower in places with lower test scores and in more segregated places (2014). Both of these are consistent with a story in which the quality of local schools shapes opportunities for mobility: in segregated areas, poor children are more concentrated in a subset of high-poverty schools; these schools may be lower in quality, leading to lower test scores, which reduce future educational opportunities and may be reflected in lower wages. But the evidence is far from definitive. Indeed, in another paper, Chetty and his colleagues show that children’s neighborhood contexts when they are young are more influential than their neighborhood conditions after age ten, a finding that suggests schools may not play a central role in shaping mobility (Chetty, Hendren, and Katz 2016).
In short, the evidence is increasingly clear that educational opportunity and social mobility vary spatially. Less clear, however, is the role of schooling in shaping those patterns. Local contexts shape academic skills and human capital, but how? I provide evidence to help answer that question by describing evidence of the timing of these effects. By measuring average academic skills at different ages in each school district, I provide information on how educational opportunity varies by age across communities.
Temporal Patterns of Educational Opportunity
Suppose we characterized each community on two dimensions of opportunity: opportunities available to children in early childhood and opportunities available during their middle childhood. Early opportunities might depend on experiences that children have in their homes, in childcare, and in preschool. These will be strongly influenced by the average family resources in a community (income, social capital, educational attainment), but may also depend on neighborhood conditions and local context. For example, two equally poor communities may differ in the extent to which children are exposed to lead paint or other environmental toxins. Two equally affluent communities may differ in the quality of available preschool programs. Middle childhood opportunities may depend substantially on children’s schooling experiences and the quality of the local schools, but also may be shaped by family resources and neighborhood conditions, the availability of afterschool activities, neighborhood safety, and so on.
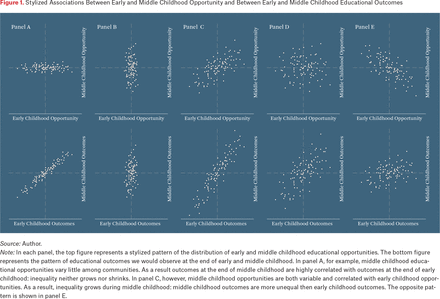
Given these two dimensions, consider five potential patterns of the distribution of educational opportunities among communities. Each of these five corresponds to a panel in figure 1, and each is characterized by three features: the variance of early childhood opportunities, the variance of middle childhood opportunities, and the correlation between the two. The top portion of figure 1 illustrates patterns of early and middle childhood opportunities; the bottom portion shows the corresponding stylized patterns of outcomes at the end of early and middle childhood that would result.
Stylized Associations Between Early and Middle Childhood Opportunity and Between Early and Middle Childhood Educational Outcomes
Early experiences largely shape outcomes. In this case, early childhood educational opportunities vary widely among communities, but middle childhood opportunities are similar across places. This might occur if, for example, early opportunities depend heavily on private resources (parental income and investments of time and money in children’s development) and middle childhood opportunities are structured by public institutions (such as schools) that are much more equal in the opportunities they provide than are families. This pattern would be consistent with the view that schools are equalizing forces in society, at least relative to out-of-school experiences.
Middle childhood experiences largely shape outcomes. In this case, educational opportunities in early childhood are much less variable than those in middle childhood. This might occur if school quality were highly variable but preschool quality and parenting practices were not related to family resources. Such a scenario is admittedly not very likely given what we know about the world and the substantial impact of family resources on early childhood opportunities and development (Duncan and Brooks-Gunn 1997; Phillips and Shonkoff 2000).
Both early and middle childhood opportunities vary considerably and are positively correlated. Here, there is really only a single dimension of opportunity: communities where children have above-average early opportunities tend to be those where middle childhood opportunities are also high, and vice versa. This might occur if school quality depended on average family socioeconomic resources, for example, or if family resources continue to play a powerful role in children’s educational development while they are in school. In this scenario, inequality of outcomes would grow from early to middle childhood.
Both early and middle childhood opportunities vary considerably, but are uncorrelated. In this case, the factors that shape early childhood opportunities (such as family resources, preschool quality, environmental hazards) are not the same as those that shape later opportunities (such as schools or afterschool programs). As a result, in some communities both early and middle childhood opportunities are high; in some both are low; and in some one is high and the other low. The presence of two distinct temporal dimensions of opportunity would suggest that strategies for improving opportunity might need to be targeted by both age and place.
Both early and middle childhood opportunities vary considerably and are negatively correlated. In this case, middle childhood experiences tend to be compensatory. Those communities that provide low opportunities early in childhood—because of, for example, low family resources or few or low quality preschools—do provide high opportunities later, and vice versa.
In the remainder of this article, I construct a version of figure 1 empirically. Specifically, I use aggregated test score data to construct two measures for each school district in the United States: a measure of average third-grade test scores (which can be thought of as the result of educational opportunities prior to third grade), and a measure of average learning rates from third grade to eighth grade (which can be thought of as the result of educational opportunities during late elementary and middle school). The underlying data represent virtually all U.S. third through eighth graders’ scores on state accountability tests from 2009 to 2015. I use these data to construct measures of average initial (third grade) test scores and growth rates of average scores in each district. Essentially, I partition each district’s average eighth-grade scores into two components—initial third-grade levels and growth from third through eighth grade. This partition provides information about the temporal structure of educational opportunity in each school district.
DATA
The test score data I use come from the Stanford Education Data Archive (SEDA), which includes estimates of the average test scores—by school district, grade, year, subject, and race-ethnicity—of students in almost every public school district in the United States (Reardon, Ho et al. 2017). These estimates are based on roughly three hundred million state accountability test scores (taken by roughly forty-five million students) on math and English language arts (ELA) tests in grades three through eight from 2009 through 2015 in every public school district in the United States. The SEDA data are publicly available.2 Cells with fewer than twenty students are suppressed in public SEDA data.
The SEDA data are constructed from administrative data, but are not simple tabulations of administrative records. The raw test score data used to construct the SEDA data come from the federal EDFacts data collection system, which were provided by the National Center for Education Statistics under a restricted data-use license. The data include, for each public school in the United States, counts of students scoring in each of several academic proficiency levels, often labeled along the lines of below basic, basic, proficient, and advanced. These counts are disaggregated by race-ethnicity, grade (grades three through eight), test subject (math and ELA), and year (school years 2008–2009 through 2012–2015).
Using these proficiency category counts, my colleagues and I estimate average scores in each school district. The algorithm is described in the SEDA documentation (Fahle et al. 2018). Charter schools’ test scores are included in the public school district in which they are formally chartered or, if not chartered by a district, in the district in which they are physically located. Thus, here I conceptualize a school district as a geographic catchment area that includes students in all local charter schools as well as in traditional public schools. Virtual schools—online schools that do not enroll students from any well-defined geographic area—are dropped from the sample. Such schools enroll fewer than half of 1 percent of all students in the United States.
The test scores in each state, grade, year, and subject are placed on a common scale so that performance can be meaningfully compared across states, grades, and years. First, each state’s test scores are linked to the math and reading scales of the National Assessment of Education Progress (NAEP). The NAEP scale is stable over time and is vertically linked from fourth to eighth grade; this allows comparison of test scores among districts in different states and within a district across grades or years. Second, the NAEP scale is transformed linearly to facilitate grade-level interpretations. In this new scale, the national average fourth-grade NAEP score in 2009 is anchored at 4; the national average eighth-grade NAEP score in 2013 is anchored at 8. A one-unit difference in scores is interpretable as the national average difference between students one grade level apart (for much more detail on the linking method and scale, see Reardon, Kalogrides, and Ho 2016). Details on the source and construction of the estimates are available on the SEDA website.
Any description of test score growth or change depends on the test metric used. The NAEP scale (or the linear transformation of it used here) is useful because it was developed to allow comparisons over time, across states, and across grades. Nonetheless, it is not the only defensible scaling of test scores. Another potential metric is one in which test scores are standardized relative to the national student test score distribution within each grade. In this scale, the average test score in each grade is 0 and the standard deviation is fixed at 1 in each grade. This is useful for comparing the relative magnitude of differences in test scores in one grade to another grade but may distort information about relative growth rates. If the variation in true skills grows over time, the standardized metric will necessarily compress that growth and bias it toward zero, inducing a negative correlation between initial status and growth. Here I use both the NAEP metric (rescaled to grade-equivalent units) and a standardized metric, though I focus primarily on the vertically linked NAEP metric because it allows meaningful changes in variance across grades. I use the standardized metric as a sensitivity check.3
Estimating Average Test Scores and Growth in Average Test Scores
Each school district includes as many as eighty-four grade-year-subject specific measures of average test scores (six grades, seven years, and two subjects). I use these estimates to construct measures of the average performance of students in a given grade (pooling across years and subjects) and the within-cohort growth rate of average scores across grades (pooling across cohorts and subjects). This approach is conceptually similar to that used by Paul Hanselman and Jeremy Fiel in their study of test score growth rates among California schools (2017).
First, I define a cohort of observations as the set of observations corresponding to sequential grades in sequential years. Therefore, for example, one cohort is composed of students in third grade in 2009, fourth grade in 2010, fifth grade in 2011, and so on, through eighth grade in 2014. The next cohort consists of those in third grade in 2010 (eighth grade in 2015), and so on. Formally, I define a cohort as the spring of the year in which a group of students would have been in kindergarten (so that cohort = year – grade); thus the 2005 cohort describes students who were in kindergarten in spring of 2005 (and who therefore appear in the SEDA data from fourth grade in 2009 through eighth grade in 2013). Twelve cohorts are represented in the SEDA data, from the 2001 cohort (in eighth grade in 2009) through the 2012 cohort (in third grade in 2015).
Note that this definition of cohort does not necessarily correspond to a constant group of students. That is, the students in eighth grade in 2014 in district d are not the same set of students who were in third grade in district d in 2009. Some students may have been retained in grade or skipped a grade; some may have left the district; others may have moved in. Such in- and out-migration may add random or systematic noise to our estimates of average growth rates; we may underestimate growth in places where those who leave are disproportionately higher-achieving than those who move in. Conversely, we may overestimate growth in places with the opposite in- and out-migration patterns or with high retention rates. This is a limitation inherent in the raw EDFacts data, which do not include student longitudinal records.
Let 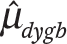 and ωdygb = se(
and ωdygb = se(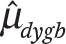 ) indicate the estimated average test score and its standard error for students in district d in year y , grade g, and subject b. Let grd ∈ (3,4,5,6,7,8) and coh∈ (2001,…,2012) be continuous measures of grade and cohort, and let math∈ (0,1) be a binary indicator variable denoting the subject of an observation. Using data from all districts, years, grades, and subjects, I fit versions of the following precision-weighted multilevel model:
) indicate the estimated average test score and its standard error for students in district d in year y , grade g, and subject b. Let grd ∈ (3,4,5,6,7,8) and coh∈ (2001,…,2012) be continuous measures of grade and cohort, and let math∈ (0,1) be a binary indicator variable denoting the subject of an observation. Using data from all districts, years, grades, and subjects, I fit versions of the following precision-weighted multilevel model:
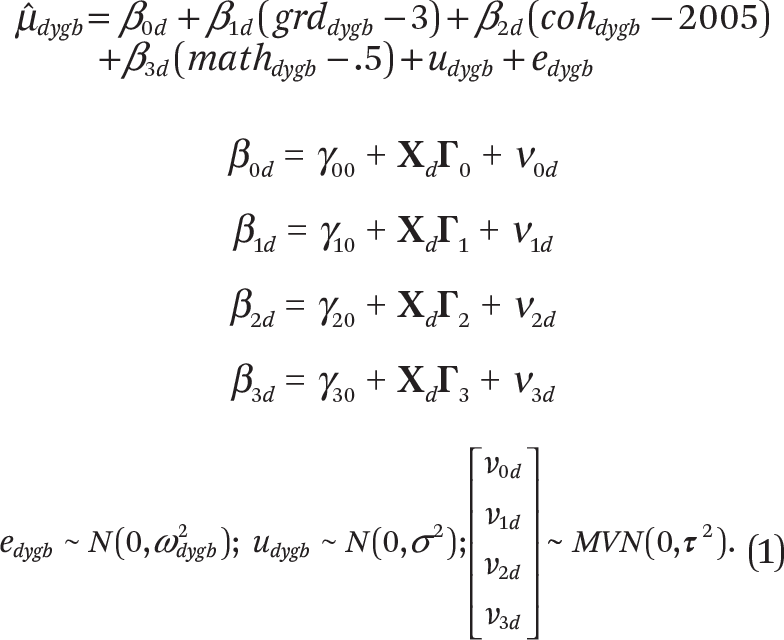
I fit these models via maximum likelihood, treating 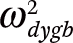 as known (it is the square of the standard error of
as known (it is the square of the standard error of 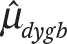 ). The variance term σ2 and the τ2 matrix are estimated.
). The variance term σ2 and the τ2 matrix are estimated.
I first fit this model with no district-level covariates ( Xd). This model provides estimates of a number of parameters of interest: the average third-grade test score in each district d (β0d), the average within-cohort growth rate of test scores from grades three to eight in district d (β1d), the variances of these two parameters in the population of all districts, and the correlation between grade-three average scores and growth rates. Given the stated framework, we can think of β0d as a measure of the average educational opportunities children in district d have prior to the end of grade three. Likewise, we can think of β1d as a measure of the average educational opportunities children have to learn the tested material between grades three and eight. The predicted average test scores in district d in eighth grade are therefore the sum of average grade-three scores and five years of growth: β0d + 5β1d.
Because 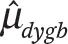 is scaled to have an average value of 4 among fourth graders in 2009 and an average of 8 among eighth graders in 2013, the coefficients β0d and β1d reflect grade-level units. Note that β0d = 3 implies that students in district d have the same average scores in third grade as the average 2008 third grader in the United States. Likewise, β1d = 1 implies that students in district d have the same average learning rate from grade three to grade eight as the average U.S. student in the 2005 cohort. A value of β1d = 1.1 or β1d = 0.90 , for example, would imply that the performance of the average student in district d improves or declines, respectively, 10 percent (one-tenth of a grade-level per year) faster or slower, respectively, than the average U.S. public school student from the third to the eighth grade.
is scaled to have an average value of 4 among fourth graders in 2009 and an average of 8 among eighth graders in 2013, the coefficients β0d and β1d reflect grade-level units. Note that β0d = 3 implies that students in district d have the same average scores in third grade as the average 2008 third grader in the United States. Likewise, β1d = 1 implies that students in district d have the same average learning rate from grade three to grade eight as the average U.S. student in the 2005 cohort. A value of β1d = 1.1 or β1d = 0.90 , for example, would imply that the performance of the average student in district d improves or declines, respectively, 10 percent (one-tenth of a grade-level per year) faster or slower, respectively, than the average U.S. public school student from the third to the eighth grade.
Of particular interest here is the joint distribution of β0d and β1d. This is given by 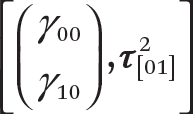 , where
, where 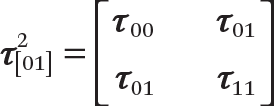 is the 2-x-2 upper-left submatrix of τ2. This joint distribution is our primary focus: τ00 and τ11 describe the variances of β0d and β1d, respectively, and their correlation is computed as r01 = τ01 (τ00 · τ11)–1/2. Note that I estimate the covariance matrix
is the 2-x-2 upper-left submatrix of τ2. This joint distribution is our primary focus: τ00 and τ11 describe the variances of β0d and β1d, respectively, and their correlation is computed as r01 = τ01 (τ00 · τ11)–1/2. Note that I estimate the covariance matrix  via maximum likelihood using the model above, rather than from the observed variances and covariance of the estimated (and therefore error-prone) β0d’s and β1d’s.
via maximum likelihood using the model above, rather than from the observed variances and covariance of the estimated (and therefore error-prone) β0d’s and β1d’s.
In addition to providing estimates of the parameters of the joint distribution of β0d and β1d, the model also provides estimates of β0d and β1d for each district. I use the Empirical Bayes (EB) shrunken estimates of these parameters, denoted 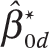 and
and 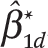 . The model provides estimates of the reliability of each of these estimates as well as a measure of their average reliability.
. The model provides estimates of the reliability of each of these estimates as well as a measure of their average reliability.
The other coefficients in the model are of less direct interest for our purposes here: β2d indicates the average within-grade (cohort-to-cohort) change per year in average test scores in district d; β3d indicates the average (within grade and year) difference in math and reading scores in district d.
To estimate the association between district characteristics (denoted by the vector Xd) and average test scores (β0d) and test score growth (β1d), I fit models that add Xd as predictors of the district parameters in model (1).
Measuring Average Socioeconomic Status Among Enrolled Students
To measure the socioeconomic characteristics of the families of children, I use data from the American Community Survey (ACS). The ACS includes detailed sociodemographic data for families living in each U.S. school district; these tabulations are available through the School District Demographic System (SDDS). I use data from the 2006–2010 SDDS tabulations because they include tabulations of family characteristics among families with school-age children enrolled in public schools.
In particular, I use six measures of the socioeconomic composition of families living in a district with children enrolled in public schools: median family income; percentage of adults with a bachelor’s degree or higher degree; poverty rate; unemployment rate; Supplemental Nutritional Assistance Program eligibility rate; and percentage of families headed by a single mother. Each of these is available separately by race-ethnicity (for racial-ethnic groups of large enough local population size).
I construct a measure of each district’s average socioeconomic status as the first principal component of the six measures. This measure is standardized to have a mean of zero and a standard deviation of 1. To give a sense of how this measure is scaled, table 1 describes the average characteristics of school districts at various values of the socioeconomic status (SES) composite.
Average Family Socioeconomic Characteristics, at Various District SES Composite Values
ANALYTIC SAMPLE
The data I use here include 11,315 school districts for which I am able to compute a socioeconomic status variable and for which the SEDA data include measures of academic achievement. Districts not included in the sample are predominantly very small districts for which samples are too small for SDDS to report socioeconomic characteristics or that have fewer than twenty students total per grade (in which case the SEDA data do not include estimates of average test scores). The ACS SES variable cannot be constructed for 824 districts; these are small districts (averaging forty-three students per grade) and contain fewer than 1 percent of U.S. public school students. The districts in the analytic sample collectively enroll roughly 3.7 million students per grade (roughly 99 percent of all U.S. public school students).
How Do Grade-Three Average Scores and Growth Rates Vary Among Districts?
Model 1 provides estimates of the average grade-three test scores and the average grade-three through grade-eight growth rate in each district. It also provides maximum likelihood estimates of the variances and correlation of these parameters. Recall that we can think of the grade-three test score average as a measure of early educational opportunities in a district; the growth rate serves as a proxy for growth opportunities—the extent of educational opportunities in grades three to eight (though these opportunities may occur in and out of school).
Table 2 presents the parameters describing the joint distribution of these two measures. The left panel reports the results based on the preferred grade-equivalent NAEP scale; the right panel reports comparable results based on the standardized scale. Each panel includes a column for math and ELA score, as well as results from the model that pools the data and estimates a common grade-three level and growth rate for both subjects.
Characteristics of the Joint Distribution of Grade-Three Test Scores and Grade-Three Through Grade-Eight Growth Rates
In the average school district, third-grade average test scores are roughly one-sixth of a grade level above the national average, and increase by 0.97 grade levels per grade.4 By third grade, test scores vary substantially across school districts. The standard deviation of district average third-grade scores is almost one grade level (0.98 grade levels), meaning that roughly one-third of school districts have average third-grade test scores more than one grade level above or below the national average (one-sixth above and one-sixth below).
Perhaps surprisingly, the correlation between average third-grade scores and growth rates is very weak—and negative (r = –0.13). This means that knowing a district’s average third-grade scores tells us almost nothing about the rate at which average scores change from third to eighth grade. Or, in terms of opportunity structure, the communities where children experience high opportunities to learn in early childhood and early elementary school are not necessarily those where opportunities to learn are high in the elementary and middle school years, and vice versa.5
The weak and negative correlation between grade-three levels and growth rates does not imply no association between eighth-grade scores and growth rates. Because average eighth-grade scores are in part the result of growth rates, we would expect them to be positively correlated with growth rates, and they are, though the correlation is moderate (r = 0.49). This suggests that eighth-grade average scores carry more signal regarding growth rates than third-grade scores. However, if we estimate the correlation between growth rates and average scores across all grades three through eight (which is more typical of the level of detail publicly available about schools), the correlation is small (r = 0.21).
The right panel of table 2 repeats the analysis using the standardized test score scale. In this scale, the correlation between growth rates and grade three average scores is similar, but slightly more negative than the estimate based on the grade-equivalent NAEP scaled scores. Again, average opportunities prior to third grade are a poor predictor of average growth rates.
One additional feature of table 2 is worth noting. The second and third columns of each panel show the estimate separately for math and reading tests. Between-district variation in growth rates is much higher in math scores than in reading (the standard deviation [SD] of growth rates is 40 percent larger in math than in reading), and—at least in the NAEP scale results—much less in third-grade achievement in math than in reading (the SD is 15 percent smaller in math than reading). This is consistent with the commonly held belief that math skills are more affected by schooling, and that reading skills are affected by both home and school environments. Early childhood and early elementary opportunities to learn to read may be more variable than opportunities to learn math skills, but growth in math scores from grade three to eight appears to vary much more than growth in reading scores. Moreover, the correlation of growth and eighth-grade scores is much higher for math than for reading (r = 0.69 for math versus r = 0.21 for reading). In other words, eighth-grade math scores are a reasonably good proxy for growth rates in math, potentially because students’ math skills (particularly those measured by standardized math tests) are shaped largely by opportunities to learn during the elementary and middle school years.
That said, in the interest of parsimony, I focus for the remainder of this article on models that pool the estimates across math and reading. Given the relatively high within-district correlations between math and reading grade-three scores (r = 0.90) and between math and reading growth rates (r = 0.66), models that pool the results across subjects capture most of the relevant information. Moreover, although growth rates and grade-three levels are estimated reliably in all of the models here (generally above 0.75), they are lower in the subject-specific models than the pooled models (where the grade-three averages are estimated with reliability 0.96 and the growth rates with reliability 0.86). The higher precision of the pooled models allows for sharper distinctions among districts. Although differences may indeed be important in those factors that shape opportunities for math and reading skill development, those issues are outside the scope of this analysis.
How Much Do Growth Rates Vary?
It is clear from table 2 that average test scores in grade three are uninformative as predictors of growth rates, perhaps because variation in growth rates is relatively small. It is useful therefore to quantify the magnitude of the variation in growth rates. The standard deviation of growth rates is 0.135 grade levels per year, or equivalently, 0.675 grade levels from grade three to grade eight. This means that in roughly one-sixth of districts test scores improve by two-thirds or more of a grade level from grades three to eight; in another one-sixth of districts scores fall behind by two-thirds or more of a grade level. Another way to quantify this is that a growth rate of 1.135 indicates that students’ scores increase 13.5 percent faster than the national average (an increase of 13.5 percent of a school year is roughly an additional twenty-five school days per year in the typical district, not a trivial amount). So variation among school districts in average growth rates is considerable.
Another way to quantify the relative magnitude is to compare the magnitude of between-district variation in growth rates to that of between-district variation in grade-three test scores. Consider two school districts, one in which students’ third-grade scores are at the national average but growth rates are 1 standard deviation above the national average; and one in which students’ third-grade scores are 1 standard deviation above the national average but growth rates are at the national average. In which district are students’ scores higher by eighth grade, and by how much? These calculations are shown in the bottom panel of table 2.
A standard deviation difference in growth rates experienced over five years from grade three to grade eight is equivalent to a 70 percent of a district standard deviation in grade-three levels. That is, in five years, students in the average-early-opportunity and high-growth-opportunity district make up 70 percent of the grade-three gap relative to a high-early-opportunity and average-growth-opportunity district. These results hold in both the reported scales.
Where Are Growth Opportunities Highest?
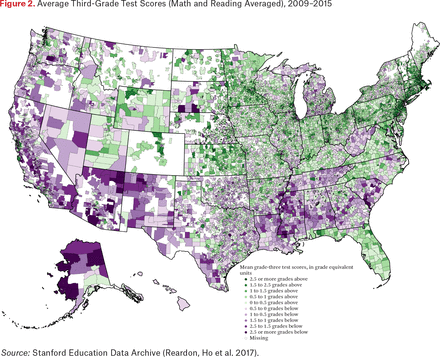
Figures 2 and 3 display the geographic patterns of grade-three average scores and grade-three through grade-eight growth rates. Figure 2 shows that opportunities prior to grade three are highest in many of suburban and exurban school districts around metropolitan areas, particularly in the Northeast, Midwest, and the California coast, and are low in much of the Deep South and the rural West. Growth opportunities in contrast are more varied. Tennessee is characterized by moderately low third-grade scores but above-average growth rates; Florida, by contrast, is characterized by slightly above-average scores in grade three but very low average growth.
Average Third-Grade Test Scores (Math and Reading Averaged), 2009–2015
Average Test Score Growth Rates (Math and Reading Averaged), 2009–2015
Table 2 and figures 2 and 3 indicate considerable variation in both grade-three average scores and growth rates, but no high correlation between the two. This is more evident in figure 4, which plots each district’s estimated growth rate (on the vertical axis) against its grade-three through grade-eight growth rate. The plot uses the EB estimates 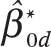 and
and  ; imprecisely estimated values are shrunken toward the overall mean. Note that district estimates with a reliability less than 0.7 are not included in this or other figures (though their data are included in fitting model 1).
; imprecisely estimated values are shrunken toward the overall mean. Note that district estimates with a reliability less than 0.7 are not included in this or other figures (though their data are included in fitting model 1).
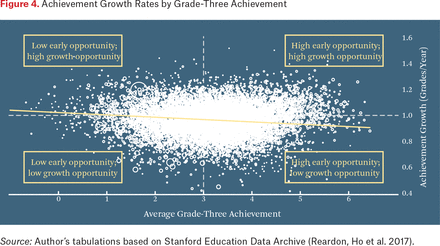
Achievement Growth Rates by Grade-Three Achievement
Figure 4 makes the very weak relationship between average third-grade test scores and average growth clear. The figure can be divided into four quadrants defined by districts’ early educational opportunity and growth opportunities. In the upper right are districts characterized by high early educational opportunity and high growth opportunity, districts where students have high average achievement in grade three and above-average growth rates after grade three. In the lower left are districts characterized by the opposite pattern: low early and low growth opportunity. The off-diagonal quadrants have high early and low growth or low early and high growth opportunity structures, respectively.
The striking feature of figure 4 is the absence of a correlation between growth and initial scores. Among districts with high grade-three scores are many with high growth and many with low growth; the same is true among those with low initial scores. This suggests the lack of a significant floor or ceiling effect in the estimates (which is not surprising, given that the data points reflect district average scores not individual student scores). Even among school districts with very high scores in third grade (three grade levels above average), some districts have very high growth; the same is true among initially low-performing districts.6
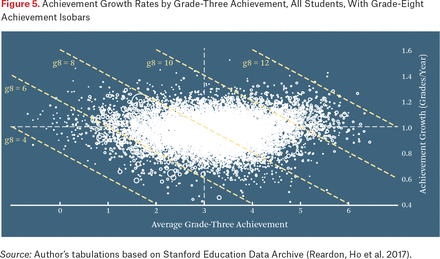
Another perspective on figure 4 is provided by considering districts with the same eighth-grade average scores. The lack of a substantial correlation between growth and grade-three scores implies that, among districts with the same eighth-grade average scores, some have higher grade-three scores and lower growth and others have lower initial status and higher growth. Figure 5 illustrates this: the plot is the same as figure 4, but includes lines representing levels of grade-eight average achievement drawn as isobars on the plot. Districts that fall anywhere on an isobar have the same average eighth-grade achievement, despite differences in initial status and growth rates. For example, a district where initial scores are one grade level below average and the average growth rates is 1.2 will have the same average eighth-grade scores as one where initial scores are one grade level above average but growth rates are 0.8 (both districts will fall on the g8 = 8 line).
Achievement Growth Rates by Grade-Three Achievement, All Students, With Grade-Eight Achievement Isobars
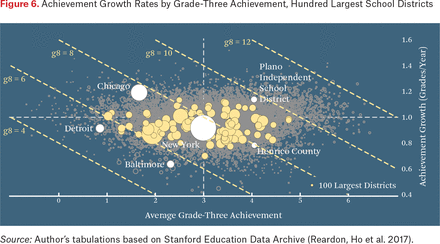
Chicago, for example (see figure 6), has average third-grade test scores well below the national average (about 1.4 grade levels below), but very high growth rates. New York City students have both average third-grade scores and average growth rates. And in Henrico County (suburban Richmond), Virginia, third-grade test scores are very high but growth rates are very low. As a result, eighth-grade scores in Chicago, New York, and Henrico County are quite similar (within a half grade level of each other) despite a range of 2.5 grade levels difference in their third-grade scores. Likewise, Detroit and Baltimore eighth-grade test scores are quite similar to one another (and very low, more than 2.5 grade levels below the national average), but in Baltimore the low eighth-grade scores are more the result of low growth opportunities than low early opportunities, the opposite of Detroit.
Achievement Growth Rates by Grade-Three Achievement, Hundred Largest School Districts
Figure 6 highlights the hundred largest school districts in the United States. The substantial variation among them on both the early and growth opportunity dimensions suggests that the variation evident in figures 3 through 5 is not simply the result of idiosyncratic variation among small school districts or sampling noise. Each of these districts’ estimates are based on hundreds of thousands or millions of test scores (Chicago’s is based on more than two million, for example).
How Is Average Test Score Growth Related to District Socioeconomic Status?
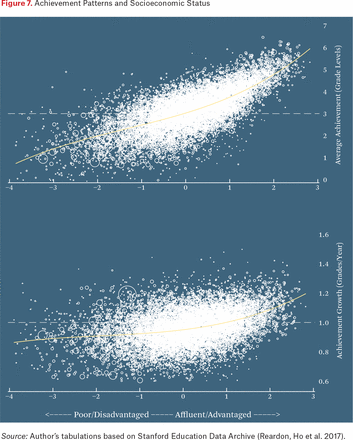
Figure 7 displays the association between the socioeconomic status measure and both grade-three average scores (upper figure) and growth rates (lower figure). The fitted lines are estimated from a version of model 1 that includes a cubic function of socioeconomic status (SES) as a predictor of each of the four district-level parameters in the model. SES is positively associated with grade-three scores and growth rates, but the association is much stronger with grade-three average scores (r = 0.68) than with growth rates (r = .32). These associations are presented in figure 7.
Achievement Patterns and Socioeconomic Status
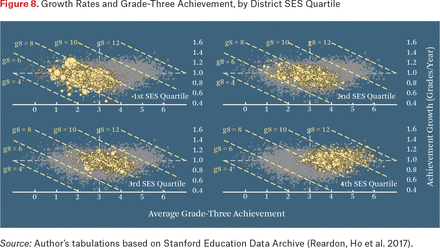
It may seem strange that both grade-three average scores and growth rates are higher, on average, in high-SES districts than in low-SES districts, but the scores and growth are slightly negatively correlated. Figure 8 helps clarify these patterns. Each panel of the figure highlights districts in a given SES quartile. Low-SES districts have generally, but not always, low average scores, and many have lower than average growth rates. High-SES districts, in contrast, generally have above-average scores, but above-average growth rates only slightly more often than below-average growth rates. In sum, socioeconomic status distinguishes where districts fall on the x-axis of figure 8 but is not especially predictive of where districts fall on the y-axis.
Growth Rates and Grade-Three Achievement, by District SES Quartile
Levels and Growth for Poor and Nonpoor Students
How Do Growth Rates Vary by Student Poverty Status, Race-Ethnicity, and Gender?
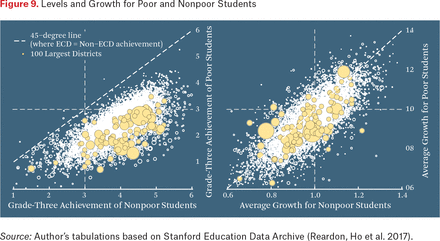
The preceding analyses demonstrate considerable variation among school districts in both early educational opportunities (as measured by average third-grade test scores) and in growth rates from grade three to grade eight. How do these patterns differ by students’ poverty status, race-ethnicity, and gender? Figure 9 displays average third-grade test scores (left panel) and growth rates (right panel) for poor and nonpoor students.7 The left panel compares the average third-grade scores. On average, poor students’ average third-grade scores are 1.5 grade levels below those of their nonpoor peers in the same district. Moreover, despite considerable variation in the gap in average third-grade scores between poor and nonpoor students, almost every district falls well below the 45-degree line in the figure. Of the roughly ten thousand school districts for which we have enough data to estimate average achievement levels by poverty status, in only a handful do poor and nonpoor students arrive in third grade with equal academic skills (and in most of those few cases, both poor and nonpoor students have low third-grade scores).
The right panel shows that the pattern is quite different when comparing poor and nonpoor students’ growth rates. In most school districts, poor students’ growth rates are quite similar to those of nonpoor students in the same district (most of the districts fall near the 45 degree line). The average within-district difference in growth rates between nonpoor and poor students is 0.04 grade levels per year. That is, in the average district, poor students have third-grade scores roughly 1.5 grade levels below their nonpoor peers and fall behind by an additional 0.2 grade levels by eighth grade. The difference in the early (before grade three) opportunities of poor and nonpoor students is much larger than the average difference in opportunities to learn in grades three to eight.
Table 3 reports the joint distributions of districts’ grade-three average test scores and growth rates by subgroup. Each column describes the distributions for a different group—by poverty status, race-ethnicity, and gender. The top row reveals the large differences in early educational opportunity by poverty status and race-ethnicity: poor students’ average scores are 1.5 grade levels below those of nonpoor students in third grade. The racial-ethnic disparities are similarly large: the white-black and white-Hispanic gap are also roughly 1.5 grade levels in third grade.
Characteristics of the Joint Distribution of Grade-Three Test Scores and Grade-Three Through Grade-Eight Growth Rates, by Subgroup
The second panel of table 3 reports average growth rates. The average growth rate of poor students in the average district is 0.04 grade levels per year lower than that of nonpoor students. The white-black difference in growth rates is -0.055. These are meaningfully large, but not enormous, differences; they imply that the poor-nonpoor and white-black gaps grow by roughly 0.20 to 0.25 grade levels between third and eighth grade, a modest increase relative to the size of the gaps in third grade.8 The Hispanic average growth rate is actually slightly higher than the white growth rate, meaning that white-Hispanic gaps narrow very slightly (by about one-eighth of a grade) between third and eighth grade. The Asian average growth rates are substantially higher, on average, than any other group, almost 0.15 grade levels per year higher than white growth rates. In the average district, Asian students have average scores roughly 0.7 grade levels higher than white students in grade three. This gap doubles, on average, by eighth grade.9
The last two columns report growth rates by gender. Girls have, on average, both higher third-grade scores and higher growth rates than boys. By eighth grade, girls’ average scores are roughly half a grade level higher than boys. Other research indicates that this difference is primarily due to the fact that girls substantially outperform boys on ELA tests, by nearly a grade level in eighth grade (Reardon et al. 2018).
Figure 10 summarizes the joint distribution of average third-grade scores and growth rates for each subgroup (the gender figures are not shown because the male and female patterns differ relatively little from one another relative to the racial-ethnic and socioeconomic differences). In most school districts, poor students, black students, and Hispanic students all have below-average test scores in third grade; nonpoor, white, and Asian students more commonly have above-average scores. The growth rate patterns differ somewhat. Black students, for example, are generally in districts where both their early opportunities and growth opportunities are low (lower left quadrant). The pattern is not so pronounced for Hispanic students and poor students: in many districts they have above-average growth rates despite below-average third-grade scores. More generally, figure 10 makes clear that patterns of both early opportunity and growth opportunity vary substantially by poverty status and race, but that growth opportunities are sometimes quite high for poor and Hispanic students.
Growth Rates and Grade-Three Achievement by Subgroup
DISCUSSION, PART ONE: THE POTENTIAL AND LIMITS OF ADMINISTRATIVE EDUCATION DATA
The data I use here, like most administrative data, are the residuum of a set of federal and state educational bureaucratic processes; they were not designed and collected with social science research needs in mind. Each state tests all students in grades three through eight, and reports their scores—in aggregated and coarsened form—to the U.S. Department of Education through the EDFacts system because federal law requires it. As a result, the data have both advantages and limitations.
Perhaps the most significant feature of the EDFacts data is their population coverage; the data are based on the test scores of the full population of public school students in grades three to eight in each year from 2008–2009 through 2014–2015 (with some missing data, as noted). Roughly twenty-two million third through eighth graders are enrolled in public school each year in the United States; each takes both a math and ELA test. Over the seven years of data I use, therefore, states administered roughly three hundred million tests to these students. This is more than a hundred times as many tests as administered by NAEP over the same period: roughly six hundred thousand math and reading tests in grades four and eight in each of the years 2009, 2011, 2013, and 2015. Even a school or district with only twenty-five students per grade would be represented by more than two thousand test scores (7 years x 6 grades x 2 subjects x 25 students = 2,100 tests) in the EDFacts data, versus only roughly sixteen in the NAEP data. The EDFacts data therefore can provide a high-resolution description of test score patterns even in very small schools or school districts.
The full population coverage of the EDFacts data make it possible to identify both general patterns of academic performance (such as the magnitude of achievement gaps) and heterogeneity in these patterns among subgroups, schools, districts, grades, and years. Sample-based analyses (even large samples like NAEP) might be able to provide reliable estimates of average test scores and growth rates for the nation as a whole, and by subgroup, or even by state (as is possible with NAEP data), but are generally inadequate to describe the heterogeneity of these patterns across smaller geographic or organizational units, like school districts. As the analyses show, heterogeneity in these patterns among school districts is considerable.
One additional benefit of these data is that they are not just publicly available but also identifiable and linkable to other data. Each school district in the public SEDA data is identified by name and by a unique NCES ID that can be used to merge the data to other data, public and private. As a result, these data allow us not only to quantify the variation among school districts in the key parameters of interest here, but also to identify interesting cases or sets of cases to study further. For example, we might be interested in what community and school characteristics foster high test score growth rates for poor students. We could identify a set of school districts in which poor students’ growth rates are high, and then collect additional data, through case studies, about these districts; such case studies might be used to generate causal hypotheses that could be systematically tested in a larger set of districts. In addition, the data can be linked to available data on local policy and context to study the effects of educational and social policies on academic achievement (for examples of papers using the SEDA data to study the effects of social policy and conditions, see Shores and Steinberg 2017; Sorensen et al. 2018; Torats-Espinosa 2018).
That said, the EDFacts data are far from ideal in a number of ways. First, the test scores are based on tests that differ across states and grades, and sometimes across years, making them not readily comparable except within a given state-grade-year. Second, the scores are coarsened—reported in broad categories with labels such as basic, proficient, and advanced. Not only does the coarsening destroy some information, but the categories are also not defined in comparable ways across states, grades, and year. Third, the EDFacts data are reported in aggregated form, as counts of students in a given subgroup, school, grade, and year who score in each of two to five ordered performance categories; the EDFacts data do not include individual student records. This has two drawbacks: it is not possible to link students’ scores longitudinally or across subjects in the same grade and year; and no data on individual student characteristics are included in the data. The latter means that we can tabulate the test scores only according to the subgroups reported in the data (which are those that states are required to report by law: race-ethnicity, gender, economic disadvantage, and so on); we cannot construct student-level cross-tabulations (race-by-gender, for example).
These limitations are not trivial. The comparability issues due to differences in states and the definition of coarsened performance categories would seem to damn any attempt to compare performance except within individual state-grade-year-subjects. Further, the coarsening of the data would seem to muddy any statistical comparisons between the test score distributions in different districts, even in the same state-grade-year-subject, because the means and variances of each district’s score distribution are not reported. My colleagues and I, however, demonstrate that it is possible to recover reliably estimated test score means and variances in each district-grade-year-subject, and then to link these to a common national scale that enables meaningful comparisons across all districts and across grades and years (Reardon, Kalogrides, and Ho 2016; Reardon, Shear et al. 2017). Using these methods, we constructed the estimated district-specific test score means I use in this article. These estimates are publicly available through the Stanford Education Data Archive.
One additional hurdle constrains the usefulness of the EDFacts data for research purposes. The raw EDFacts data are not publicly available; they require researchers to obtain a restricted data-use license from the National Center for Education Statistics. Moreover, to avoid disclosure of individually identifiable information, researchers are required to send all analyses to NCES for review before dissemination or publication. The raw EDFacts data are unsuppressed, meaning that even if a single student of a given subgroup is in a particular school-grade-year, that student’s test score is reported in the raw EDFacts data files. NCES reviews research findings prior to dissemination to ensure that no individually identifiable information is released publicly. To enable us to make the estimated test score distributions publicly available through SEDA, NCES and EDFacts provided us with a blanket disclosure agreement. Under this agreement, we suppress any estimate based on a cell size of fewer than twenty test scores. In addition, we add a small amount of random noise to all reported estimates to ensure that the estimation algorithm cannot be reverse-engineered to recover the underlying cell counts. With these provisos in place, NCES allows us to release our estimates publicly without further disclosure review. Because of this agreement, we are able to publicly disseminate estimates of the distributions of test scores in grades three through eight from 2009 through 2015, all measured on a common scale, in virtually every U.S. school district. These data are available at the Stanford Education Data Archive.
Despite the value of SEDA, the available data cannot, however, overcome the limitations caused by the lack of student-level longitudinal data. Such data do, of course, exist. Most states now have education data systems that track individual students over time as long as they remain in the state’s public education system. One could, in theory, use states’ student-level longitudinal data files (and the continuous, uncoarsened test scores they contain) for research, as many scholars have done. The challenge, however, is in negotiating data-use agreements with each of the fifty states; without fifty separate data agreements, the use of student-level longitudinal data comes at the cost of full population coverage. Ideally, states might work together to create common systems for sharing de-identified individual educational records that would make it possible to conduct longitudinal student-level analyses with full population coverage; until that time, researchers will face a trade-off between using inferior data with full population coverage or more complete data in samples or subsets of the population.
DISCUSSION, PART TWO: THE HETEROGENEITY OF OPPORTUNITY
As noted, one of the advantages of having data on the full population of students, as opposed to a relatively small sample of students or districts, is that both general patterns and variation become clear. The analyses demonstrate several key facts, some of which would not be evident without data of this kind.
First, variation is enormous among districts in the extent of early learning opportunities available to children before third grade. These differences are evident in the wide range of average third-grade test scores. Not surprisingly, early opportunities are strongly associated with districts’ socioeconomic characteristics; affluent families and districts are able to provide much greater opportunities than poor ones early in children’s lives.
What may be surprising, however, is the extent of variation among communities in the kinds of opportunities they provide for students to learn from grades three to eight, and that these growth opportunities are at best weakly correlated with early opportunities and socioeconomic status. This is consistent, however, with other work showing that patterns of achievement do not correspond closely to patterns of test score growth (Hanselman and Fiel 2017). The empirical patterns presented earlier are most similar to the scenario described in panel D of figure 1: both early and middle childhood opportunities vary widely among school districts, but do not covary significantly.
It is tempting to think of growth rates in test scores as a rough measure of the effectiveness of a district’s public schools. This is neither entirely inappropriate nor entirely accurate, however. The growth rates better isolate the contribution to learning due to experiences during the schooling years than the grade-three scores. Grade-three average scores are likely much more strongly influenced by early childhood experiences than the growth rates. Growth rates are therefore certainly better as measures of educational opportunities from age nine to fourteen than average test scores in a school district are. But that does not mean they reflect only the contribution of schooling. Other characteristics of communities, including family resources, afterschool programs, and neighborhood conditions may all affect growth in test scores independent of schools’ effects. Thus, some caution is warranted in interpreting the average growth rates as pure measures of school effectiveness. Nonetheless, relative to average test scores (at grade three or any other), the growth rates are certainly closer to a measure of school effectiveness. Given that schooling plays a significant role in children’s lives from age nine to fourteen (at least in terms of time spent), it is not unreasonable to think that the growth measures carry some signal regarding school quality—and more signal than contained in simple average test score measures.
If we take the growth rates, then, as rough measures of school effectiveness, then neither socioeconomic conditions nor average test scores are especially informative about school effectiveness in a district. Many districts with high average test scores have low growth rates, and vice versa. Similarly, many low-income districts have above-average growth rates. This finding calls into question the use of average test scores as an accountability tool or a way of evaluating schools. Because average test scores, even in eighth grade, are only weakly correlated with growth rates, any system that rewards or sanctions schools or districts on the basis of their average scores will necessarily do so inappropriately in many cases (assuming that we wish to incentivize growth rates). Any information system that makes average test scores publicly available to parents in the hopes that a market for high test score districts will emerge and drive school improvement may instead simply create a market for high-SES districts, increasing economic segregation without improving school systems. To the extent that public information about school quality affects middle- and high-income families’ decisions about where to live, information on growth rates might provide very different signals, perhaps leading to lower levels of economic residential and school segregation.
That is not to say the growth rates of the type I have calculated here—using repeated cross-sectional aggregated data—are ideal, but they almost certainly are better signals than average test scores of the learning opportunities available in a school district. If we used measures like these as one part of an accountability system or a public information system, school districts in the upper-left quadrant of figure 4 would be preferred (at least in grades three through eight) over districts in the lower-right quadrant. Future research might compare the growth measures I construct here with those based on longitudinal student-level data. Such measures would be immune from the potential noise in my measures that arises because of district in- and out-migration or grade retention, or both.
The findings here also provide some insight into the issues raised in the opening of this paper. Are schools engines of opportunity or agents of inequality? The answer is perhaps more nuanced than the question implies. Some school districts seem to provide high opportunities for children from low-income families during elementary and middle school; others do not. This suggests that our school systems (or other community institutions) have the potential to catalyze opportunity, but that potential is incompletely realized in many places. And although poverty is systematically associated with low opportunities to learn in early childhood, as evidenced by the consistently low average third-grade test scores in low-income districts, poverty very clearly does not strictly determine the opportunities for children to learn in the middle grade years. That said, it is not clear from the patterns here that an effective school system alone can make up for low opportunities in early childhood. The large gaps in students’ academic skills between low- and higher-SES districts are so large that even the highest growth rate in the country would be inadequate to closing even half of the gap by eighth grade.
These patterns have implications both for education policy and for our understanding of the potentially equalizing role of schools. In terms of policy, they suggest that levels of student outcomes are a poor measure of school effectiveness. I am certainly not the first to say this, but the data from eleven thousand school districts demonstrate the point very clearly. The findings also suggest that we could learn a great deal about reducing educational inequality from the low-SES communities with high growth rates. They provide, at a minimum, an existence proof of the possibility that even schools in high-poverty communities can be effective. Now the challenge is to learn what conditions make that possible and how we can foster the same conditions for children everywhere.
APPENDIX: SCALE SENSITIVITY OF CORRELATIONS BETWEEN GROWTH AND STATUS
The correlation between initial status (grade-three test average test scores in our case) and growth (change in average scores from grade three to grade eight here) is sensitive to the relative scales in which initial and final scores are measured. To see this, let Y3 and Y8 represent scores in grades three and eight, respectively. Let Δ = Y8 – Y3 the change in scores. Let τ3 = Var(Y3); τ∆ = Var(Δ); and C = Cov(Y3, Δ) Note that the correlation of growth and initial status is then r∆3 = Corr(Y3,Δ) = 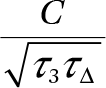 .
.
Now suppose we transform by a linear transformation, where b > 0:
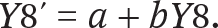
The change as measured in this new metric is
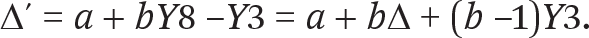
The variance of changes in the new metric is
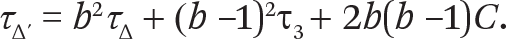
And now the correlation of Y3 and Δ′ will be
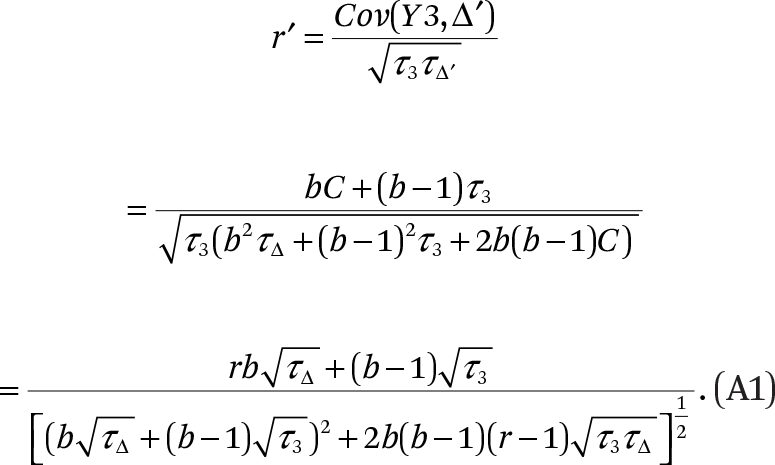
Now, given τ3, τ∆, and C (or r), r′ is a continuous, monotonically increasing function of b. Note that
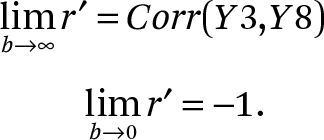
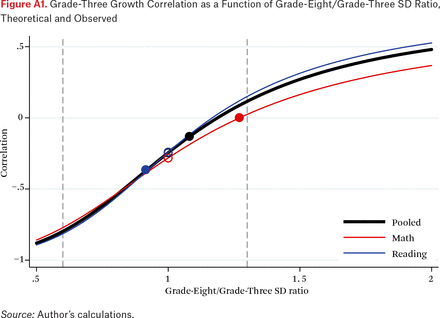
If we take the estimated values of τ3, τ∆, and C estimated from model 1 using the standardized test scale (the scale in which τ3 = τ8), we can plot the equation (A1) as a function of b (see figure A1).
Grade-Three Growth Correlation as a Function of Grade-Eight/Grade-Three SD Ratio, Theoretical and Observed
The red line, for example, displays the correlation between math average third-grade scores and growth rates as a function of b. In the standardized scale (corresponding to b = 1 on the figure), the estimated correlation is –0.282 (as shown by the hollow red circle). In the NAEP scale, the estimated correlation is 0.002, indicated by the solid red dot. This occurs at a value of about b = 1.25, which is very close to the ratio of the eighth-grade NAEP math standard deviation to the fourth-grade standard deviation. In other words, NAEP scale has a value of roughly b = 1.25 in math (and a value of b = 0.94 in reading).
To produce a correlation of r′ > 0.25, we would need b > 1.5 in reading and b > 1.7 in math. In other words, if the eighth-grade metric were stretched by a factor of 1.7 or 1.5 in reading or math, respectively, the estimated correlation would be positive 0.25 rather than –0.25—still a low correlation but with the opposite sign as we observe in the standardized scale. Is a factor of b > 1.5 plausible?
One way to assess this is to examine other vertically scaled tests. Nathan Dadey and Derek Briggs examine sixteen vertically scaled tests used in state assessment programs (2012). For these tests, the value of b—the ratio of the eighth-grade standard deviation of scores to the third-grade standard deviation—ranges from 0.6 to almost 1.3 (though most of the reading ratios are between 0.8 and 1.0; most of the math ratios are between 0.9 and 1.1). Howard Bloom and his colleagues report standard deviations for seven vertically equated reading tests; the grade-eight to grade-three standard deviation ratios in those tests range from 0.87 to 1.04 (2008). Of the twenty-three vertically scaled assessments for which data are available, none have b > 1.3. The vertical gray dashed lines in the figure show the range of values of b reported by Dadey and Briggs (2012) and Bloom his colleagues (2008). The possible correlations these values of b would produce in the SEDA data range from –0.80 to +0.15. This suggests that no plausible vertical scale would yield a moderate or high positive correlation between grade-three test scores and growth rates.
FOOTNOTES
↵1. Commuting zones are collections of counties similar to metropolitan areas but covering the entire United States. The average commuting zone includes about four counties.
↵2. Stanford Education Data Archive, http://seda.stanford.edu (accessed October 10, 2018).
↵3. Other scalings of the test metric are defensible, of course. The indeterminacy of test metrics poses a challenge to any analysis of growth rates (Bond and Lang 2013; Ho 2008; Ho 2009; Reardon 2008). For more discussion of the sensitivity of the estimates to alternative test scalings, see the appendix.
↵4. The average district’s scores are not equal to the national average for three reasons. First, more small districts have above-average test scores and slightly lower than average growth rates, so the unweighted averages across districts are not identical to the enrollment-weighted averages. Second, some very small districts are not included in the analytic sample. Third, the national average is constructed relative to students in the 2005 cohort (grade four in 2009, grade eight in 2013), but districts’ average scores are computed using all cohorts in the SEDA data (cohorts 2001 through 2012). The average third-grade scores over all cohorts were slightly higher than those in the 2005 cohort, whereas the average growth rate was somewhat lower.
↵5. As noted, this correlation is sensitive to the scale used to measure test scores.
↵6. The measures here are not subject to ceiling effects or regression to the mean for several reasons. First, the district average scores in third grade are very precisely estimated because of the large number of scores in each district; as a result, measurement-error induced regression to the mean is not a concern. Second, the district-level means are generally not near the ceiling or floor of the tests; although individual students’ scores may in some cases reach a test’s floor or ceiling, the average in district does not (even in the highest-score district, average scores are less than 1 standard deviation from the test score mean, placing the average student in that district somewhere near the 80th percentile of the state’s test score distribution—so the average student in the district still has room to improve). Third, the methods used to construct the measures rely on the ordinal nature of test scores, and so are less sensitive to floor and ceiling effects than methods based on interval scale measures.
↵7. States report test scores by students’ economic disadvantage status; each state can define economic disadvantage differently, though in practice, most use eligibility for free or reduced-price lunch to define economic disadvantage.
↵8. Hanselman and Fiel conduct a related but different analysis (2017). Using 1998 to 2002 test score data from California, they find that black, Hispanic, and Asian students attend schools where, on average, the overall average growth rates are only slightly lower than in the schools attended by white students. Their analysis does not, however, identify race-ethnicity specific growth rates, so is not directly comparable to the analyses here.
↵9. Average test score growth rates by subgroup are each estimated on a different sample of districts—those enrolling at least twenty students of that subgroup per grade. Therefore, the differences between subgroups’ estimated average growth rates in table 3 are not exactly the same as the average within-district average growth difference. One should read the differences in average growth rates here as suggestive of how achievement gaps change from the third to eighth grade, but not definitive. A better description of how gaps change (and how those rates of change are related to the magnitude of the gaps in third grade) could be obtained by limiting the analyses to a subset of districts with large enough populations of the two subgroups of interest, and then estimating the average rate of change of within-district achievement gaps in this sample of districts. That analysis is beyond the scope of this article.
- © 2019 Russell Sage Foundation. Reardon, Sean F. 2019. “Educational Opportunity in Early and Middle Childhood: Using Full Population Administrative Data to Study Variation by Place and Age.” RSF: The Russell Sage Foundation Journal of the Social Sciences 5(2): 40–68. DOI: 10.7758/RSF.2019.5.2.03. The research described here was supported by grants from the Institute of Education Sciences (R305D110018), the Spencer Foundation (Award #201500058), the William T. Grant Foundation (Award #186173), the Bill and Melinda Gates Foundation, and the Overdeck Family Foundation. The paper would not have been possible without the assistance of Ross Santy, Michael Hawes, Marilyn Seastrom, and Jennifer Davies, who facilitated access to the EDFacts data. This paper benefited substantially from ongoing collaboration with Andrew Ho, Erin Fahle, and Ben Shear and from the research assistance of Joseph Van Matre and Richard DiSalvo. Some of the data used in this paper were provided by the National Center for Education Statistics (NCES). The opinions expressed here are my own and do not represent views of NCES, the Institute of Education Sciences, the U.S. Department of Education, the Spencer Foundation, the William T. Grant Foundation, the Bill and Melinda Gates Foundation, or the Overdeck Family Foundation. Direct correspondence to: Sean F. Reardon at sean.reardon{at}stanford.edu, 520 CERAS Building #526, Stanford University, Stanford, CA 94305.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.