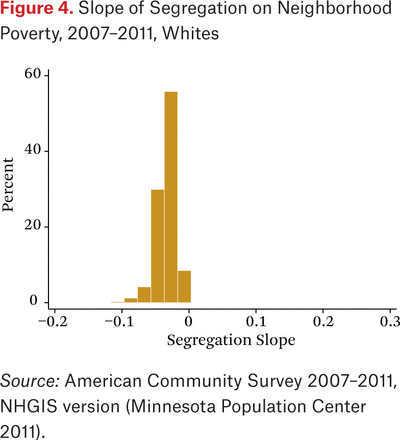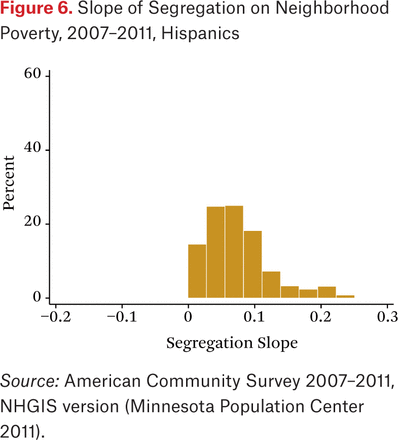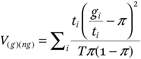Abstract
A frequently cited model of why segregation contributes to inequality is that segregation increases the level of contextual advantage of advantaged segregated groups and the level of contextual disadvantage of disadvantaged segregated groups. This paper provides a formal demographic model of this process. The model begins with two groups that differ along a dimension of average advantage and disadvantage, for instance, two racial groups that differ in their poverty rates. The model illustrates how the contextual advantages and disadvantages from segregation are affected by a series of demographic conditions: group relative size, group advantage-disadvantage rates, group effects on advantage-disadvantage rates of nongroup neighbors, and advantage-disadvantage effects on group contact. The paper outlines a series of eleven conclusions from the theoretical model and applies the theoretical model to understanding racial segregation effects on racial group neighborhood poverty contact in American cities.
Segregation has long been thought to contribute to inequality, especially racial inequality. Although a variety of explanations are typically offered for why segregation may contribute to inequality, the most common in contemporary discussions is that segregation is associated with affluent contexts for whites and impoverished contexts for nonwhites. The explanation is the primary one offered by two of the most prominent social scientists who emphasize the importance of racial segregation in producing racial inequality, Douglas Massey and Gary Orfield.1
Douglas Massey, for instance, argues that, as segregation increases, “the average residential environment of whites improves and the average residential environment of blacks deteriorates” (1990, 333). This occurs because segregation separates affluent and poor racial groups into different neighborhoods, producing racial inequality in neighborhood conditions. Massey then goes on to argue that these concentrations of neighborhood poverty are a key to the existence of an “urban underclass” and to racial inequality more generally.
Gary Orfield has made parallel arguments as applied to schools. Indeed, the main reason we should be concerned with segregation by race, he says, is because “segregation by race is systematically linked to other forms of segregation, including segregation by socioeconomic status, by residential location, and increasingly by language” (Orfield and Lee 2005, 14). He argues that segregation by race is primarily of concern exactly because it creates high-poverty schools for many minority students and high-poverty school environments are not conducive to learning.
The basic argument both these scholars make is that segregation produces neighborhoods and schools that are either predominately white and low poverty or predominately nonwhite and high poverty. In general, their logic suggests that as segregation increases, members of advantaged segregated groups increasingly experience high rates of advantaged persons in their contexts, and that members of disadvantaged groups experience high rates of disadvantaged persons. To the extent that experiencing contexts with advantaged members is itself a source of advantage and that experiencing contexts with disadvantaged members is itself a source of disadvantage—as a large body of research suggests2—segregation then increases the on-average contextual advantage of the advantaged and the contextual disadvantage of the disadvantaged. Correspondingly, several studies note the large gap in the affluence of neighborhoods and related social contexts experienced by whites, blacks, and Latinos and argue that this is an important factor contributing to persistent racial inequality (see, for example, Pattillo 1999; Logan 2011; Sharkey 2013).
Does racial segregation always increase the concentration of poverty for members of disadvantaged racial groups and affluence for advantaged racial groups? Both Massey and Orfield suggest that it does, as a necessity of the mathematical demography of the combination of segregation and racial disparities in poverty. Neither, however, develop a formal model of this process or make the mathematical demography explicit.
Yet an increase in segregation need not increase the contextual advantage of advantaged groups and the contextual disadvantage of disadvantaged groups in all situations, nor need a decrease in segregation decrease it. A prominent example of how racial desegregation can fail to reduce a disadvantaged group’s level of contextual disadvantage is William Julius Wilson’s (1987) black middle-class outmigration thesis. Wilson claims that declines in residential segregation in the 1960s and 1970s were a process by which affluent blacks moved out of poor black neighborhoods leaving poorer blacks behind (see Wilson 1987, 55–58). As a result, middle-class blacks gained white neighbors—thus making this a migration flow that reduced racial segregation—and poor blacks lost middle-class black neighbors. Overall, Wilson’s suggestion is that average black neighborhood income showed little improvement in the wake of black middle-class migration into white neighborhoods.
In this article, I consider conditions under which segregation acts more as Massey and Orfield suggest than as Wilson suggests. In effect, this analysis produces a set of scope conditions under which Massey and Orfield’s theories operate. The contribution is in developing a broader understanding of the complex factors that determine how the spatial arrangement of segregation contributes to group contextual advantage or disadvantage. The analysis clarifies spatial factors that amplify or dampen the effects of segregation on contextual advantage and contextual disadvantage via spatial arrangement. Finally, it assess the extent to which these conditions hold in contemporary U.S. metropolitan areas, and thus helps clarify the role of segregation in producing unequal neighborhood poverty rates among persons of different racial and ethnic backgrounds.
A FORMAL MODEL OF SEGREGATION AND CONTEXT
Both Massey and Orfield’s descriptions suggest the concentration of disadvantage in the neighborhoods of blacks and Hispanics is a necessary result of the mathematical demography of segregation combined with racial inequality. Neither, however, actually develops an explicit model of this process. The closest effort is a simulation model Massey developed, first published as an article in the American Journal of Sociology (1990) that later became chapter 5 in Massey and Nancy Denton’s seminal American Apartheid (1993).
Massey begins with a hypothetical city with black and white residents (only) and studies changes in poverty contact as the level of segregation changes. In his hypothetical city, the black poverty rate is 20 percent and the white rate is 10 percent. He shows that as segregation between blacks and whites is increased, holding other conditions constant, the average neighborhood poverty of whites decreases and of blacks increases. In a second simulation, he adds income segregation within race, showing that as segregation of whites from blacks increases in the presence of income segregation, neighborhood poverty contact for black poor residents increases even more sharply.
Massey’s simulations illustrate how segregation combined with racial disparities in poverty rates produce racial inequalities in neighborhood environments. But his simulation imposes several conditions that receive little direct attention in his discussion. For instance, the simulation sets the size of the two racial groups in his hypothetical city to be equal, does not allow income to affect cross-race contact, and does not allow race to affect the income level of other-race neighbors. It is unclear how the logic of segregation concentrating poverty might be changed if these circumstances are changed.
Wilson’s black middle-class outmigration thesis implies a different relationship between segregation and contextual advantage and disadvantage. In his account in The Truly Disadvantaged, the migration of middle-class blacks out of black central-city neighborhoods in the 1960s and 1970s resulted in decreased neighborhood poverty for middle-class blacks and increased neighborhood poverty for poor blacks (Wilson 1987, 53–57). Wilson is less clear about where middle-class blacks migrated to, but he suggests the suburbs, including some into white neighborhoods. In his account, racial desegregation of residence did not decrease black neighborhood poverty but instead increased it for poor blacks and reduced it for middle-class blacks.3
A key difference between Massey’s account of the effect of segregation and Wilson’s of black middle-class outmigration is that in Massey’s account desegregation occurs across all income levels, whereas in Wilson’s only middle-class blacks see an increase in white neighbors.4 This contrast suggests a broader point: income gradients in a process of segregation or desegregation are important to how segregation affects contextual inequality. An income gradient is an income-selective pattern of cross-race contact, such as high-income African Americans having more white neighbors than low-income African Americans do. If the income gradient to segregation is strong, Massey and Orfield’s basic arguments about how segregation contributes to contextual inequality may not operate.
To get more precise about the conditions under which segregation concentrates or deconcentrates poverty, I develop a formal model. This model provides a precise description of how this process occurs and details related spatial conditions that can increase or weaken the effects of segregation on concentrating advantage and disadvantage. Effectively, it can be viewed as formalizing and generalizing Massey’s theory, which suggested mathematical necessity, but without developing the math.
The decomposition discussed here is closely related to a decomposition model developed and applied to understand poverty concentration (Quillian 2012). The model examines the outcome of poverty concentration by group, or the extent to which poor members of a racial group tend to have poor neighbors. By contrast, in the analysis in this manuscript, average poverty concentration is considered for all members of a racial or ethnic group. The model then examines how segregation affects contextual advantage or disadvantage on average for the segregated groups.
Spatial Arrangement and Substantive Segregation Effects
In examining the effects of segregation on concentrating poverty, Massey’s simulations focus purely on the mathematical effect of spatial rearrangement of population when segregation is increased. Other conditions, such as group size and poverty rates, are held fixed as segregation is changed. Yet as many scholars argue—including Massey—segregation has important substantive effects on populations beyond its mechanical spatial effect on neighborhood poverty. A reduction in segregation would increase the disadvantaged group’s access to better labor markets and schools, which would decrease the disadvantaged group’s poverty rate (see, for instance, Massey and Denton 1993, chapter 6; Quillian 2014).
Following Massey’s simulations, the model I develop examines spatial arrangement effects of segregation only, omitting substantive effects. The spatial arrangement effect can be estimated precisely once the dynamics of the system are understood: they are a mathematical function of patterns of cross-group contact, as Massey and Orfield suggest. By contrast, substantive effects depend on a behavioral model with attendant uncertainties; in the literature of substantive segregation effects, estimates vary substantially. Also, spatial rearrangement effects on neighborhood poverty rates are immediate, whereas much of the behavioral effect occurs in a longer time scale gradually after segregation changes. For simplicity, in what follows I refer to spatial rearrangement effects simply as segregation effects. This omits potentially important but distinct substantive effects, which are not a focus of this article.
A Formal Population Model
The formal model considers segregation of a social group, the group, from the rest of the population, the nongroup. In the most common application, the group would be a racial or ethnic group.
In the model, aside from their group membership, individuals are either advantaged or disadvantaged. Although the dimension of advantage and disadvantage can be based on anything defined for individuals and distinct from the social groups, income is the typical dimension. Advantage or disadvantage are defined for individuals, but rates of advantage and disadvantage differ across groups. Advantaged groups are groups with low rates of individual disadvantage (and high rates of advantage); disadvantaged groups have high rates of individual disadvantage (and low rates of advantage).
In this analysis, the disadvantaged members of each group are operationalized as poor (income below the government poverty line) and the advantaged individuals as nonpoor (income above the poverty line). The group we focus on are denoted g in our models, and the poverty rate of group g is Povg. Everyone not in the focal group is in the nongroup, denoted ng. The poverty rate of the nongroup is Povng. If the focal group is disadvantaged, Povg > Povng. If the focal group is advantaged, Povg < Povng. The most obvious application is to racial groups. In the United States, blacks or Hispanics would typically be disadvantaged groups and whites an advantaged group.
Consider the average contact that members of the group and the nongroup have with poor and nonpoor persons in a social context. This context could be a neighborhood, a school, a social network, or some other setting. For the ith context (neighborhood) denote the number of poor persons (both group and nongroup) in the context as pi, the total number of persons in the context as ti, and the number of group members in the context as gi. Denote the total number of persons in the group summed across all contexts (all neighborhoods) with G. The average context of group poor persons with poor persons in their social context can be denoted using the P* index of contact popularized by Stanley Lieberson (1988):
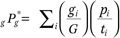
This measure can be interpreted as the average percentage poor (disadvantaged) in the contexts of members of the group. Segregation will be measured with a standardized index related to indexes of contact, the variance ratio index of segregation, as discussed further.
The theory that segregation increases contextual disadvantage for disadvantaged groups or advantage for advantaged groups effectively proposes that as segregation between disadvantaged group g and others who are not in group g (ng) increases, gP*p increases. If group g is advantaged, then gP*p will decrease with segregation, reflecting declining contextual advantage with segregation for an advantaged group.
To formalize this relationship, we need to incorporate how segregation affects the average contact with contextual poverty of the poor and nonpoor. The additive decomposability of P* indexes is useful in this regard. Average contact with poor in the social context is the sum of contact with poor of the disadvantaged group and contact with poor of who are not members of the group; although members of the nongroup have a lower poverty rate than members of the disadvantaged group, some members of the nongroup are poor:
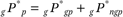
This formula includes two measures that are closely related to segregation: contact of group members with their own racial or ethnic group and with persons not of their own race or ethnic group. Segregation, however, is generally defined based on contact with all members of each group, not just their poor members. We want to introduce segregation overall to this equation but still get to a formulation with components that are substantively interpretable. To do so, first I manipulate the formula to include terms for own-group and other-group contact:
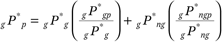
We can improve the interpretation of the ratios in parentheses by norming them by the poverty rate of each group:
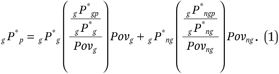
The two components in the large brackets capture what we might think of as group membership effects on contact with poor persons of their own group (left term) and poor persons of the nongroup (right term). These ratios will be greater than 1 if members of the group have disproportionate contact with disadvantaged members of their own group (left term) or disproportionate contact with nongroup persons who are disadvantaged (right term), disproportionate being defined relative to their group’s or the nongroup’s poverty rate. If they are more likely to be in contact with nonpoor member of their own group (left term) or the nongroup (right term), these ratios will be less than one.
We can relate these terms mathematically to segregation by using the variance ratio index of segregation, a measure of segregation that is in the same family of measures as the exposure indexes. The variance ratio index is a well-established measure that fits key criteria desired in a segregation index (see James and Taeuber 1985).5 Like the index of dissimilarity, the variance ratio index varies from 0 (no segregation between groups) to 1 (perfect segregation). Also like dissimilarity, the variance ratio is a measure of evenness of distribution of one group against the other (see Massey and Denton 1988).
The variance ratio index of segregation is related to the P* contact index between group members and nonmembers by the relation:

where png is the proportion of the population nongroup and V(g)(ng) is the variance ratio index of segregation between the group and the nongroup. Applying this relation to equation (1) we get:
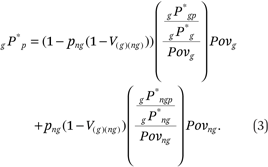
This last formula, (3), allows us to understand group neighborhood poverty contact in social context as a function of segregation (V) between the two groups and a series of other conditions: group poverty rates (Povg and Povng), group relative size (png), and the two ratios shown in the big parentheses.
The ratios in the two large parentheses in (3) each have an interpretable meaning. They indicate relative contact of group members with, first, poor group members and, second, poor persons not in the group. Denote these terms GxGP and GxNGP:

Rewriting (3) with these terms we get the following:
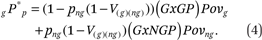
This formula is the same as (3) but GxGP and GxNGP replace the corresponding terms. Each term has an interpretable meaning. The formula in (4) is a decomposition of group contact with poor into a series of components.
These components represent:
Segregation of the group from the nongroup (V(g)(ng)).
Relative group size, indicated here by percentage nongroup (png).
The poverty rate of the group (Povg).
The poverty rate of the nongroup (Povng).
The ratio (GxGP), indicating group members have disproportionately high or low contact with poor members of their own group. A ratio greater than one suggests disproportionate contact of the group with poor own-group members, a ratio less than one suggests disproportionate contact with nonpoor group members. This captures a poverty status effect on own-group contact.
The ratio (GxNGP), indicating group members have disproportionate contact with poor persons not in their group. A ratio greater than one suggests disproportional contact of the group with poor nongroup persons. This captures a group effect on the income level of nongroup persons in contact with group members.
Note that equation (4) includes no error term: it is a decomposition, not a statistical model. We can perfectly predict the average neighborhood poverty rate of a group in any city or other area for which these components are known. The equation in a sense defines the mathematically necessary accounting relationships that Massey and Orfield’s discussions suggest underlie the process they observe.
One factor is not included in these components: a measure of within-group segregation between the poor and nonpoor. This is because within-group poverty status segregation shifts poverty contact between the poor and nonpoor of a group, but does not change average poverty contact across an entire group, which is the outcome of this analysis.
The components each represent different spatial conditions that we can manipulate to predict poverty contact of a group under hypothetical changes in some of these conditions. Some combinations of component spatial conditions are not possible—a topic I lack space to explore in detail here—but these combinations can be avoided by focusing on small changes from observed values.
What does this imply about segregation? Equation (4) shows substantial interaction—multiplication—between different factors in predicting the outcome. Terms that multiply together with segregation condition its effect, or increase or decrease the importance of segregation for increasing a group’s contact with poverty. To clarify, we can multiply out (4) and group terms interacting with segregation, which produces
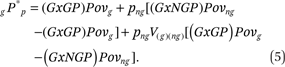
The term on the second line of (5) shows components that multiply with segregation. This term is the key to understanding effects that alter the spatial rearrangement effect of segregation on group poverty concentration. Segregation matters for poverty concentration, but its effect in producing contextual advantage or disadvantage depends on several other factors represented in this model.
This formula implies that if the other components of the formula are held constant, then the effect of segregation is linear, and the slope of segregation is as follows:
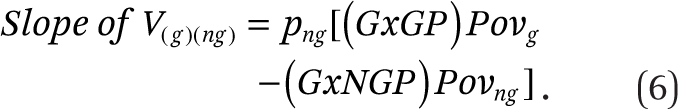
One possible application of this is to calculate the components and calculate the slope of segregation in a particular situation. For instance, using values computed for African Americans in Milwaukee from the 2007–2011 American Community Survey:
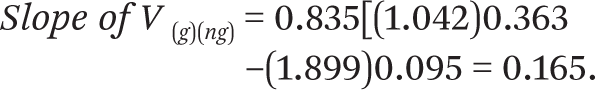
This gives an implied slope of segregation on poverty contact for blacks in Milwaukee of 0.165, holding other conditions constant, which is a large slope relative to most other segregation effects in American cities, as discussed further.
Equation (6) suggests several conclusions about segregation and poverty contact across racial groups:
Conclusion 1: Under regular conditions, segregation will tend to increase the average advantage of the contexts of the advantaged segregated group and increase the average disadvantage of contexts of the disadvantaged segregated group.
I will delay my discussion of regular conditions, but to preview, as long as the subtraction in the middle of (6) is positive and group g is a disadvantaged group, segregation will build contextual advantage and disadvantage as Massey suggests.
Conclusion 2: All else equal, the strength of effect of segregation in increasing average contextual advantage or disadvantage for a group is proportional to the difference in the level of advantage or disadvantage between the group and persons in other groups.
Segregation does not matter for group contextual advantage if the group and nongroup have the same level of advantage or disadvantage. In equation (6), this is evident from how the group poverty rate and the nongroup rate subtract.
Past accounts get this point partially incorrect by focusing on only the poverty rate of the disadvantaged group alone. In particular, Massey and Mitchell Eggers (1990) emphasize that there should be an interaction between segregation and nonwhite group poverty rates in predicting group neighborhood poverty contact. But, in fact, the interaction should be between segregation and the difference in poverty rates between the group and everyone not in that group, not the group poverty rate.
Conclusion 3: All else equal, the strength of the segregation effect on contextual disadvantage of a group is increased if the group members in contact with their own group are more often individually disadvantaged.
In the model, the ratio (GxGP) indicates how much more likely disadvantaged group members are to be in contact with their own group (g) than all group members. A ratio larger than one indicates disadvantaged persons have more own-group neighbors than the average for their group. If black middle-class migration has occurred, resulting in affluent blacks living in mostly nonblack neighborhoods and poorer blacks living in black neighborhoods, we would expect a ratio significantly above one for blacks.
A sharp own-group income gradient to segregation—in which group members who are advantaged have fewer own-group neighbors than disadvantaged group members—tends to increase the effect of the level of segregation on creating contextual disadvantage for disadvantaged groups (relative to the same level of segregation with a less-sharp income gradient to segregation) because as segregation increases in the presence of a sharp income gradient to segregation, the poorer members of the group are sorted into poor own-group neighborhoods, concentrating their contact among group members and reducing contact of nongroup members with group poverty.
In Wilson’s account of black middle-class outmigration, black racial segregation decreased and the income gradient to black segregation increased. He suggests that these two changes roughly offset each other, producing no major change in average black poverty contact. As he emphasizes, however, this increased average poverty concentration for poor blacks while decreasing it for middle-class blacks.
Conclusion 4: The strength of the segregation effect on contextual disadvantage for a group is decreased if the nongroup members in contact with group members are disproportionately likely to be disadvantaged.
Conclusion 4 is based on the (GxNGP) term in equation (6). To the extent that nongroup members in contact with group members are more likely to be disadvantaged, segregation effects are weakened because as segregation declines, group members trade disadvantaged own-group members for disadvantaged other-group members. This condition is indicated by ratios of (GxNGP) substantially above one.
Conclusion 5: The segregation effect on the focal group’s neighborhood poverty contact will be larger if a group is small in relative size.
Segregation changes more strongly influence contextual disadvantage (or advantage) when group size is relatively small. Group relative size is inversely related to the percentage nongroup, shown as Png in the slope formula of equation (6).
If a group is relatively small in size, then a change in the standardized segregation index will have more effect on contact than if a group is large. A group that is only 10 percent of the local population, for instance, will generally have many more nongroup neighbors as segregation declines and they are spread out over the metropolitan neighborhoods that are mostly composed of other-group members. By contrast, if a group is relatively large then a change in segregation will have much weaker effect on who they are in contact with. A group that is 80 percent of the population of an area will only have a moderate increase in other-group neighbors with substantially lower segregation.
Conclusion 6 (regularity conditions for conclusion 1): For a disadvantaged group g, if (GxGP)Povg > (GxNGP)Povng segregation will increase contextual disadvantage as suggested by the Massey model. For an advantaged group g, if (GxGP)Povg < (GxNGP)Povng segregation will increase contextual advantage as suggested by the Massey model.
This condition comes straight from the slope formula for segregation of equation (6).
APPLICATION
We can examine the parts of this model to assess how segregation contributes to contextual advantage or disadvantage through spatial rearrangement in a particular situation. My application of this model is to segregation between residential neighborhoods and racial groups in American cities from 2007 to 2011.
The groups in the analysis are non-Hispanic whites, blacks, and Hispanics.6 For this analysis, I define disadvantaged as poor and advantaged as nonpoor. Poverty is defined as living in a family with income below the official U.S. government poverty threshold.
I calculate the basic elements of the decomposition using data from the American Community Survey from 2007 to 2011. I use the version of the data from the National Historical Geographic Information System (Minnesota Population Center 2011). The context I use here is the neighborhood, census tracts serving as the usual proxy. Only metropolitan areas with at least twenty thousand persons in the group are used for calculating statistics by group, because segregation measures are often thought to have little meaning when groups are very small in size.
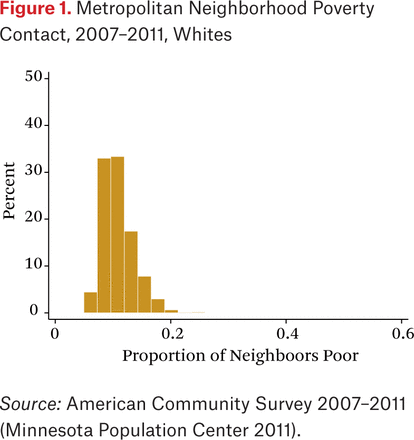
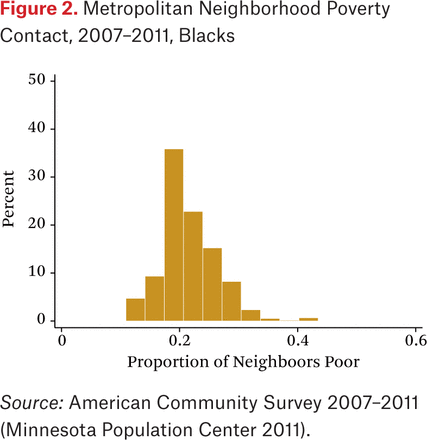
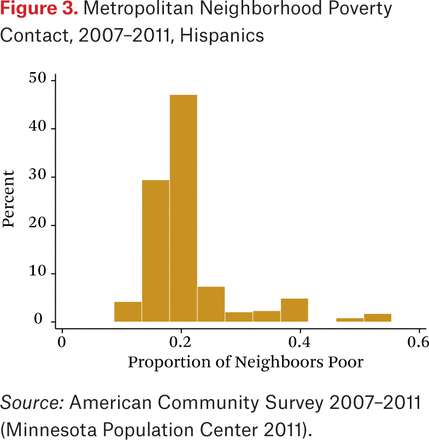
As discussed, the outcome variable is average group member contact with poor in their census tracts, gP*p, where the groups are the three racial-ethnic groups. This measure is equivalent to average neighborhood poverty rate among persons of each racial-ethnic group. Calculated separately for each metropolitan area with at least twenty thousand members of each group, the metropolitan gP*p figures are shown as histograms in figures 1 through 3. As we can see, blacks and Hispanics have significantly higher rates of neighborhood poverty contact than whites, a result also noted by John Logan (2011) and others.
I calculate the components of the decomposition formula (5) from tract data for each metropolitan area. Means of components at the metropolitan level by race and ethnic group are shown in table 1.
For GPxG, the ratios above one for blacks and Hispanics indicate that poor blacks and Hispanics have more black or Hispanic neighbors than nonpoor blacks or Hispanics. But these ratios are not very far above 1, indicating that the disparity is not very large. The white ratio below 1 indicates that, on average, poor whites have fewer white neighbors than nonpoor whites.
For GxNGP, the ratios for blacks and Hispanics deviate further from one, averaging 1.449 for blacks and 1.230 for Hispanics. What this suggests is that the other-race neighbors of blacks and Hispanics tend to have significantly higher poverty rates than the other-race average. This is highlighted in Quillian (2012): disproportionate poverty of the nongroup neighbors of blacks and Hispanics contributes importantly to high neighborhood poverty contact for these groups.
The Role of Segregation in Racial Disparities in Neighborhood Poverty Contact
The decomposition model developed earlier validates the intuition of Massey (1990) that segregation concentrates poverty, but also demonstrates that this effect depends on a set of other spatial conditions.
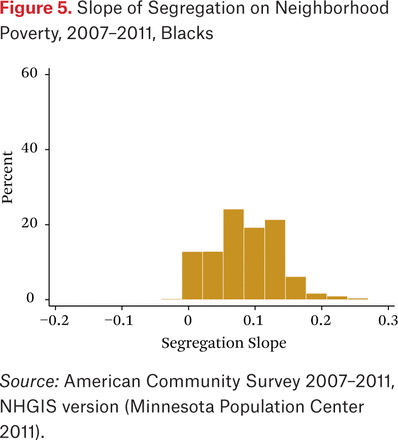
The first question I consider is whether the correct conditions hold for segregation to increase contextual advantage for whites and contextual disadvantage for blacks and Hispanics. To address this question, I calculate the slope of the segregation effect on contextual disadvantage for whites, blacks, and Hispanics for each metropolitan area from equation (6). This leads to a distribution of slopes for each group across metropolitan areas. For a 1 unit change in segregation, holding other conditions present in the decomposition constant, the slope is the indicated change in average neighborhood poverty for the group.
Table 2 shows means of the slopes by group, and figures 4 through 6 show histograms of the slopes over metropolitan areas for each group. For whites, almost all of the slopes are negative, indicating that contextual disadvantage goes down as segregation goes up. Their contextual advantage increases with segregation, indicated here by a decline in their average neighborhood poverty rate as segregation increases. Of 379 metropolitan areas (with at least twenty thousand non-Hispanic white residents), all but one have negative slopes; the exception is Honolulu.
For blacks and Hispanics almost all slopes of segregation on neighborhood poverty contact are positive. For blacks, the slope is negative rounded to two decimal places for only three of 175 metropolitan areas; for Hispanics, the slope is positive for all metropolitan areas.7 A marginal change in segregation, keeping other spatial conditions constant, increases neighborhood poverty rates for blacks and Hispanics in almost every American metropolitan area. This leads to a further conclusion.
Conclusion 7: In almost all American metropolitan areas, an increase in segregation, holding other conditions in the decomposition constant, would decrease white neighborhood poverty contact and increases black and Latino poverty contact. The conditions for segregation to build contextual advantage via spatial rearrangement among advantaged racial groups and contextual disadvantage for disadvantaged groups hold for residential segregation in almost all American metropolitan areas.
A fixed change in segregation in general has a bigger effect on increasing neighborhood poverty for black and Hispanics than decreasing neighborhood poverty for whites. As shown in figures 4 through 6, the negative slopes for whites are generally smaller in magnitude than the positive slopes for blacks and Hispanics. On average, the effect are two to two and a half times larger at increasing black and Hispanic neighborhood poverty rates than at decreasing white neighborhood poverty rates.
This is mostly a result of differences in group size (see conclusion 5). Because whites are a larger share of the population of their metropolitan areas, desegregation increases average neighborhood poverty contact only a little because other groups are too small to boost the white neighborhood poverty rate very much. By contrast, blacks and Hispanics are usually smaller shares of their metropolitan areas, with the result that decreases in segregation produce a larger percentage of nongroup members in their neighborhoods. This is another conclusion.
Conclusion 8: An increase in segregation, holding other conditions constant, would cause black and Hispanic neighborhood poverty rates to increase more than white rates drop, which largely reflects effects of group size.
A final area of investigation of the slopes relates to conclusions 3 and 4. Conclusion 3 is that segregation effects will tend to be stronger if poor group members have disproportionately more own-group neighbors. Conclusion 4 is that segregation effects will tend to be weaker if a group has disproportionately poor nongroup neighbors.
Table 2 addresses the question of how important in practice these conditions are for segregation effects. In the group decomposition model, I force the situation of no income gradient to own-race neighborhood residence: poor and nonpoor are then treated as equally likely to have own-race neighbors. As expected, this results in weaker segregation effects—the means of the slopes are closer to zero. Although the effects do get smaller, the changes are not especially large. This is not too surprising given that on average the GxGP term is close to one.
The nongroup decomposition model forces the condition that other-race neighbors have poverty rates equal to the other-race average. It shows that this condition makes a significant difference. The slopes increase in magnitude by 25 percent (Hispanics) to about 45 percent (blacks) relative to the base slopes. This yields a further conclusion.
Conclusion 9: Neighborhood segregation effects in U.S. metropolitan areas are partially suppressed because the other-race neighbors of disadvantaged group members tend to be disproportionately poor.
As segregation declines, blacks or Hispanics often trade own-race neighbors for poor other-race neighbors, weakening the reduction in contextual disadvantage with declines in segregation from other groups.
Spatial Arrangement Effects of Segregation on Contextual Advantage
How much of contextual advantage for whites, and disadvantage for blacks and Latinos, can be attributed to the spatial arrangement effect of segregation? I address this question initially by simulating a 25 percent reduction in racial segregation while holding other conditions constant based on the decomposition model. This is assuming segregation declines, but spatial patterns of how income influences cross-race contact, group relative size, and group poverty rates are unchanged by this migration.
In holding poverty rates constant, these estimates omit substantive effects. Empirical studies suggest a decline in segregation would also tend to reduce the poverty rate of the disadvantaged group, although this effect may tend to lag a change in segregation. In the spirit of the Massey (1990) simulation, I focus only on estimating the effect from spatial rearrangement with declining segregation.
The effect of a 25 percent reduction in residential segregation is estimated for all metropolitan areas by using the slope formula to estimate the change in neighborhood poverty for each group with a 25 percent segregation reduction, holding all other components of the decomposition constant. Metropolitan mean effects from this procedure are shown in table 3. Table 3 also shows effects scaled two other ways: as the percentage change in average neighborhood poverty contact relative to the metropolitan base level, and as a percentage change in average neighborhood poverty contact relative to the rate that would prevail if there was no racial inequality in poverty contact. Racial equality in neighborhood poverty contact is the situation in which each racial group on average lives in a neighborhood with the average metropolitan poverty rate.
The results show effects in the expected direction. For blacks the average slope is –0.008, which corresponds to an average change in poverty contact from base of –3.4 percent. This is a reduction in racial neighborhood inequality of 9.8 percent.8 For Hispanics the change is –0.004, or an average change from base of –2.2 percent, which is a 9.6 percent reduction in racial neighborhood inequality in poverty contact. A 25 percent decrease in segregation then moves the black and Hispanic rate about 10 percent of the way toward the level that would hold if there were racial equality in poverty contact. As conclusion 9 states, a 25 percent reduction does not produce more change, in part because of the disproportionate poverty of the other-race neighbors of blacks and Hispanics.
These are metropolitan averages and hide considerable heterogeneity in the effects. Table 4 shows the effects of segregation on poverty concentration from this procedure for cities in which these effects tend to be largest. Some metropolitan areas have conditions that produce larger segregation effects. In these metropolitan areas, effects are significantly larger, changing average poverty contact by 3 percent to 8 percent from base, which produces reductions of racial inequality in neightborhood poverty rates of 7 percent to 15 percent.
Conclusion 10: A 25 percent decrease in racial segregation, holding other factors constant, produces reductions in racial inequality in neighborhood poverty of 9 to 10 percent from base due to change in spatial arrangement. The effects are not larger because of the effects of other spatial conditions like the segregation of blacks and Hispanics from more affluent other-race neighbors.
The cities for which segregation effects are largest, shown in table 4, are also worth attention. The largest white contextual advantage effects from segregation are typically found in cities in the South and Texas border cities. These areas tend to have high nonwhite poverty rates and large shares of their population nonwhite. Segregation under these conditions especially shields whites from neighborhood poverty.
Black neighborhood poverty rates are most elevated by segregation in former industrial cities, disproportionately in the Midwest, such as Milwaukee, Detroit, Cleveland, Chicago, and Cincinnati. Two primary reasons explain this phenomenon. First, these cities tend to have the highest black-nonblack segregation scores—giving them large changes corresponding to a 25 percent decrease. Second, these cities tend to have high black poverty rates and low to moderate nonblack poverty rates.
Hispanic neighborhood poverty rates tend to be most sensitive to change in segregation in several northeastern cities. These tend to be areas with relatively small Hispanic populations and high poverty rates for their Hispanic residents.
Conclusion 11: The neighborhood poverty reduction to whites from segregation, holding other conditions constant, tend to be largest in midwestern, southern, and Texas border cities. The neighborhood poverty increase for blacks from an increase in segregation tends to be largest in midwestern cities. The neighborhood poverty increase for Hispanics from an increase in segregation tends to be largest in northeastern cities.
Effects from Eliminating Racial Segregation
Finally, I consider a last counterfactual to assess segregation effects: estimated levels of poverty contact if racial segregation was in fact zero (no racial segregation at all). In this circumstance, every tract has the same percentage of each group.
This is an extremely strong counterfactual. With zero racial segregation, many of the other parameters in the model are also necessarily zero (or one in cases where that indicates no effect). For instance, the average poverty rate of other-race neighbors for any racial group must be the same as the nongroup average in this circumstance, implicitly forcing GxGP to be one.
I calculate the effect on group poverty rates from a change to zero segregation by taking the metropolitan poverty rate overall (across all groups), and then the difference between each group’s actual metropolitan neighborhood poverty rate and this rate. In complete racial integration, each groups’ poverty contact is equal to the overall metropolitan poverty rate.
The corresponding averages are shown in table 5. These effects are much larger than those in table 3. We might expect them to be four times as large as the estimates in table 3—because table 3 was based on a 25 percent reduction—but because this zeros out related conditions (there can be no tendency of blacks to have poorer nonblack neighbors than whites on average when integration is perfect) these effects are significantly larger. White contact with neighborhood poverty increases by 28 percent in this scenario, black poverty contact decreases by 34 percent, and Hispanic contact decreases by 21 percent.
Conclusion 12: Without racial segregation there would be no metropolitan differences in neighborhood poverty exposure across racial groups, which correspond to increases (whites) or decreases (blacks, Latinos) of 20 to 34 percent in average neighborhood poverty contact, holding group poverty rates constant.
CONCLUSION
By separating groups with unequal poverty rates into different contexts, segregation builds contextual advantage for advantaged groups and disadvantage for disadvantaged groups. This basic point is illustrated famously in Massey’s (1990) simulations. Massey’s model, however, does not include other spatial conditions regarding group poverty rates and spatial patterns through which income is related to cross-race contact that can alter or, if strong enough, invert Massey’s predicted segregation effects.
The model developed here provides a more detailed specification of Massey’s simulation model, showing multiple factors interact with segregation in determining contextual advantage and disadvantage levels experienced by segregated groups. The extent to which a change in the level of segregation contributes to contextual advantage and disadvantage depends on several other conditions, notably group relative size, effects of individual advantage or disadvantage of group members on group contact, and the advantage/disadvantage level of the nongroup members whom group members are in contact.
In the spirit of Massey’s (1990) simulations, the estimates here only capture the spatial arrangement effects of segregation. Because a reduction in segregation would in the long term probably reduce black and Latino poverty rates, the overall effect of a long-term reduction in segregation is underestimated in these results. Nevertheless, the spatial arrangement effect is basic to understanding segregation effects on the social contexts of segregated groups, and can be understood with greater precision than substantive effects.
A potential application of the model is to understand how and why race group neighborhood poverty changes as migration and other processes shift group spatial patterns. A change in group neighborhood poverty between decades, for instance, could be decomposed into how different parts of the decomposition have changed, providing a deeper understanding of the changing spatial position of race and income groups that shift group neighborhood poverty.
In the case of American cities, I find that the conditions for segregation to contribute to a reduction in white neighborhood poverty rates and an increase in black and Latino poverty rates hold for almost all metropolitan areas. This analysis verifies Massey’s broad account of segregation’s role in accounting for racial disparities in neighborhood poverty contact in American cities, even without accounting for substantive ways that segregation feeds back to increase the poverty rates of disadvantage groups.
We might expect from Massey’s original model that a decrease in segregation would produce a nearly one-for-one proportionate decrease in black and Latino neighborhood poverty, together with a proportionate increase in white neighborhood poverty, which in fact specifications in Massey’s test of these ideas imply (Massey and Eggers 1990). The model reveals instead that the average marginal effect of segregation on racial disparities in neighborhood poverty rates, holding other conditions constant, are smaller than directly proportionate. A 25 percent decrease in segregation produces on average about a 10 percent decrease in neighborhood poverty inequality for blacks and Latinos. This is primarily because the other-race neighbors of blacks and Hispanics are significantly poorer than the nonblack and non-Hispanic average, and this reduces the effect of marginal changes in segregation on poverty contact. These results imply that the trend of gradually declining racial segregation in American metropolitan areas (Logan and Stults 2011) will then not reduce poverty as much in black and Latino environments as a straight application of Massey’s simulation would suggest.
Such an outcome suggests that policies to reduce racial segregation with the goal of reducing concentrations of poverty in black and Latino neighborhoods need to attend to the income character of desegregation. If only higher-income blacks and Latinos enter whiter environments, reduction in neighborhood poverty among blacks and Latinos overall may not follow. Likewise, if the white neighbors of blacks and Latinos have high poverty rates, then the poverty deconcentrating effect of a reduction in segregation is reduced. By contrast, desegregation and neighborhood poverty deconcentration are increased when lower-income blacks and Latinos move into nonpoor white neighborhoods, suggesting that siting of public housing and assistance for voucher holders to enter white low-poverty neighborhoods can have especially strong effects of reducing racial segregation and racial inequality in neighborhood poverty contact.
If we consider the strong counterfactual of no racial segregation, racial segregation effects on poverty concentration through spatial arrangement are quite large for most American cities. Although this is a strong counterfactual—it is difficult to imagine what American metropolitan areas would be like without any racial segregation—it also illustrates the important way that neighborhood racial residential segregation is a critical condition to produce unequal neighborhood income conditions across racial and ethnic groups.
FOOTNOTES
↵1. This point is not entirely original to Massey and Orfield. Their work extends previous scholarship, most notably Kenneth Clark (1989).
↵2. If affluent neighborhoods tend to have low crime and good neighborhood schools, and high-poverty neighborhoods high crime and bad neighborhood schools—as much research indicates (Coleman 1966; Peterson and Krivo 2010)—then crime and poor neighborhood schools are then also concentrated in nonwhite neighborhoods by segregation. Likewise, an increasingly convincing body of knowledge finds that neighborhood poverty is associated with long-term disadvantages for disadvantaged children that profoundly reduce their chance of upward social mobility (Wodtke, Harding, and Elwert 2011; Chetty et al. 2014; Chetty, Hendren, and Katz 2015).
↵3. Wilson does not use the term desegregation in discussing black middle-class outmigration, but middle-class black migration into white neighborhoods is a process that must contribute to racial desegregation.
↵4. Massey’s argument is buttressed by the findings of Denton and Massey (1989) that in the 1970s middle-class blacks were not much less segregated from whites than low-income blacks. More recent evidence suggests middle-class blacks are significantly more likely to live in nonblack neighborhoods than poorer blacks (Sharkey 2014).
↵5. The variance ratio index is defined as
 where gi denotes the population of the racial group in the ith tract, ti is the total number of persons in the ith tract, T is the total population of the metropolitan area for which the measure is calculated, and π is the group proportion of the population in the metropolitan area.
where gi denotes the population of the racial group in the ith tract, ti is the total number of persons in the ith tract, T is the total population of the metropolitan area for which the measure is calculated, and π is the group proportion of the population in the metropolitan area.↵6. Non-Hispanic whites are persons who identify themselves as white (alone, selecting no other-race category) on the census race question and indicate they are not of Hispanic origin. Blacks are respondents who identify as black alone on the race question, including black Hispanics. The category Hispanic includes everyone who indicates Hispanic origin. The black and Hispanic categories overlap somewhat. Poverty counts in the American Community Survey are not provided separately for non-Hispanic blacks.
↵7. The metropolitan areas with negative black slopes are Springfield, Massachusetts; El Paso, Texas; East Stroudsbourg, Pennsylvania; and New York City. These slopes are relatively very small, and the slope for New York is nearly zero (–0.005).
↵8. The reduction in racial neighborhood inequality percentage is the change in poverty contact divided by the difference between group poverty contact and group poverty contact if all groups experienced equal neighborhood poverty (in which case all groups would experience the average metropolitan poverty rate).
- © 2017 Russell Sage Foundation. Quillian, Lincoln. 2017. “Segregation as a Source of Contextual Advantage: A Formal Theory with Application to American Cities.” RSF: The Russell Sage Foundation Journal of the Social Sciences 3(2): 152–69. DOI: 10.7758/RSF.2017.3.2.07. Direct correspondence to: Lincoln Quillian at l-quillian{at}northwestern.edu, Department of Sociology, Northwestern University, 1810 Chicago Avenue, Evanston, IL 60208.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.