Abstract
Do legislators represent the rich better than they represent the poor? Recent work provides mixed support for this proposition. I test the hypothesis of differential representation using a data set on the political preferences of 318,537 individuals. Evidence of differential representation in the House of Representatives is weak. Support for differential representation is stronger in the Senate. In recent years, representation has occurred primarily through the selection of a legislator from the appropriate party. Although the preferences of higher-income constituents account for more of the variation in legislator voting behavior, higher-income constituents also account for much more of the variation in district preferences. In light of the low level of overall responsiveness, differential responsiveness appears small.
Few issues in the study of representation have garnered more attention in recent years than the link between economic inequality and political inequality. The majority view in this literature argues that government responds to the preferences of large segments of the population that are higher income much more than it responds to large segments of the population that are lower income (Bartels 2009; Bonica et al. 2013; Butler 2014; Gilens 2012; Gilens and Page 2014). This finding implies that even though citizens are equal in their ability to vote, they are unequal in their ability to incentivize politicians to take particular policy positions. That this difference remains even after accounting for different rates of voting (Bartels 2009) begs the question of why legislators would ignore a substantial portion of the people to whom they owe their jobs and continued reelection.
The approach pioneered by Larry Bartels (2009) is useful for answering this question. Bartels examines the dyadic relationship between legislators and different classes of constituents within their districts. He supposes that legislators vote according to the wishes of their mean voter, as per various “mean voter theorems” (see, for example, Caplin and Nalebuff 1991; Schofield 2007). If this is the case, then each citizen should receive equal weight in a legislator’s voting decision, just as each quantity is weighted equally in the calculation of an arithmetic mean. Groups should be weighted in correspondence with their individual size. Given a set of non-overlapping groups, this assumption leads to a clear specification for determining whether legislators do weight groups equally: assume that legislator positions are a function of the positions of the mean of each group multiplied by each group’s relative size, but allow the actual weights to vary.
However, representing the mean voter is not the only way that legislators may make their decision. The mean voter theorem replaces the older and more prominent theory of representation of the median voter (Black 1948; Downs 1957). If legislators represent the median voter, they may have equal regard for all of their constituents, but nonetheless some will seem to receive more “weight” than others—in particular, those constituents who vary more or are otherwise more likely to determine the location of the median. Yet another way in which legislators may represent their districts is via the mediating effects of party (Campbell et al. 1966). Voters may simply choose a candidate of the party they prefer, and conditional on choosing the right party, legislators may be bound only by the standards of loyal behavior within that party. If legislators have this degree of latitude, then whichever group is most likely to determine the balance of party support within a district will appear to have the greatest weight, despite an equal regard for all voters by the legislator.
In this paper, I test the hypothesis of differential representation in the U.S. House of Representatives and the U.S. Senate. For some House sessions I am able to replicate the existing result of differential representation using a large data set of political preferences. However, I also show, following two recent papers using other data sources (Bhatti and Erikson 2011; Brunner, Ross, and Washington 2013), that this result is not robust and depends on whether the slope or the fit of the model is thought to be a better indicator of responsiveness. More importantly, I show that these models do not necessarily imply large substantive differences in legislator positions resulting from differential representation. In univariate models, all groups are substantially predictive of the position that legislators will take.
In the Senate, I consistently find a stronger relationship between the preferences of richer constituents and the positions of legislators. The coefficients are somewhat uncertain, however, owing to very high multicollinearity. This finding is consistent with prior work that finds greater representation of the rich in the Senate (Bartels 2009). Nonetheless, the results highlight one of the concerns of Yosef Bhatti and Robert Erikson (2011), namely, that the preferences of various income groups are difficult to separate statistically.
In direct contrast to the mean voter theorem—the theoretical assumption underlying Bartels’s (2009) empirical specification—legislator positions were relatively homogenous within parties and heterogenous across parties from 2000 to 2012, and that continues to be true as of this writing. Partisan theories of representation are a reasonable alternative that do a better job of matching this empirical reality. Perhaps groups are unequal in the extent to which they determine the party of their representative. This result leads to a different empirical specification of party, not legislator position, as the dependent variable (Brunner, Ross, and Washington 2013). In the latter part of the paper, I show that this specification leads to a similar conclusion. The positions of both low-income and high-income constituents explain the party of their representative reasonably well in the House, with more evidence of differential representation in the Senate. The slope of this relationship is steeper for higher-income constituents. Discriminating between different explanations for legislator behavior is a difficult task that is beyond the scope of this paper. Nonetheless, the fact that these two very different approaches give similar results is a useful starting point.
These results should be understood in the context of broader political realities. The correspondence between the political preferences of constituencies writ large and the preferences of their representatives is remarkably weak, particularly when party is accounted for (Clinton 2006; Tausanovitch and Warshaw 2013). During a period when Congress has polarized dramatically, the distribution of the public’s preferences has remained centrist and stable, highlighting this disconnect (Fiorina and Abrams 2012; Hill and Tausanovitch 2015). In other words, responsiveness at an aggregate level appears to be poor. This is not surprising in light of recent evidence that casts doubt on the notion that a significant number of voters choose candidates on the basis of policy (Tausanovitch and Warshaw 2014). Furthermore, few voters are aware of the policy stances of their particular representatives above and beyond differences between the two parties (Tausanovitch and Warshaw 2014).
In light of these findings, one might wonder whether disaggregating constituents into high- and low-income groups could provide an explanation. After all, if legislators respond only to high-income constituents, then “averaging in” lower-income constituents will create the appearance of weaker representation. The results reported here show that this does not appear to be the case. Separating groups by income and introducing income itself as an additional variable does not appear to substantially improve our ability to predict the positions that legislators will take.
In the section that follows, I explain the methodology I use to estimate policy positions. Then I go on to describe the data underlying the analysis. The next two sections present the results on mean voter representation and on partisan representation, followed by the conclusion.
MEASURING PREFERENCES
One of the core difficulties in measuring policy preferences is that statements of preferences on individual issues may not accurately reflect underlying attitudes. Respondents may make top-of-the-head judgments based on immediately available considerations (Zaller 1992), or their choice may be affected by purely idiosyncratic or irrelevant factors (see, for example, Achen and Bartels 2012). One possible solution to this problem is to aggregate preferences in some way. Multiple (putatively) independent indicators of political preferences are less affected by random noise than a single response. Research has shown that using multiple indicators increases the predictive power of voters’ attitudes on outcomes such as vote choice (Ansolabehere, Rodden, and Snyder 2008).
The most commonly used methods for measuring underlying positions from revealed preference data are item response models, which conceptualize preferences as a continuous latent variable in an underlying preference space. Individual choices depend on the choosers’ latent preferences and the features of that particular choice. One of the simplest cases is a one-dimensional quadratic utility binary response model (Clinton, Jackman, and Rivers 2004). Let xi denote person i’s latent ideology, and yij denote personi’s response to question j, where yij = 1 indicates a “yes” response and yij = 0 indicates a “no” response to question j. Then the probability that person i will respond “yes” to question j is
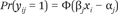
where Φ is the standard normal cumulative distribution function, and αj and βj are the item parameters for question j. βj captures the direction of the item (is “yes” a liberal or conservative response?) as well as how strong the relationship is between responses to the item and underlying preferences. αj captures the underlying liberalism or conservatism of the item (how liberal does one typically have to be to respond “yes” or “no”?). The model is identified by restricting the xi’s to have mean 0 and standard deviation 1, and the direction is fixed so that negative values are liberal.
This simple model allows us to estimate preferences and take account of the fact that some questions are more informative than others in different parts of the preference space. I estimate this model using a Bayesian approach, with dispersed normal priors for each of the estimated parameters. Unfortunately, it is quite computationally expensive to run in standard implementation. Using software developed with Jeffrey B. Lewis of UCLA, I parallelize a Markov chain Monte Carlo estimate of this model using data augmentation. In each iteration of the Markov chain, posterior draws from the distribution of the item parameters and person parameters can be made independently. We conduct these draws simultaneously on graphical processing units (GPUs), allowing us to achieve speeds thirty-two times faster than standard implementations of this model. Using this software, I am able to estimate latent preferences for a data set of 318,537 survey respondents, containing 5,084,676 nonmissing responses to 264 items.
There are numerous advantages to using a continuous measure of political preferences based on responses to policy questions, but the most important one is that a continuous measure of preferences simply gives us more information about the location of individuals in the policy space. This may be the reason that Bhatti and Erikson (2011) are able to find differential representation in the Senate using the 9,253 respondents to the American National Election Study (ANES) with a seven-point measure of ideological self-placement, but unable to find differential representation using the 155,000 respondents to the National Annenberg Election Survey (NAES) with a five-point measure. The less granular measure does not distinguish as well. An added benefit of the measurement strategy used here is that using multiple items may mitigate measurement error.
DATA
Analyzing representation requires data on the policy preferences of constituents and the legislators who represent them. Data on the former come from six large-sample political surveys: the 2000 and 2004 National Annenberg Election Surveys, and the 2006, 2008, 2010, and 2012 Cooperative Congressional Election Studies (CCES). Combined, these studies provide responses from 318,537 individuals over this period of twelve years, for an average of 732 respondents in each of the 435 congressional districts.
The household income of respondents is self-reported on each survey in a series of categories. However, the categories differ across the NAES and CCES, and the sixteen CCES categories were changed in 2012. When the categories were consolidated into four groups, they perfectly coincided, with the exception of the 2012 CCES. These four groups comprise those making less than $25,000, those making $25,000 to $49,999, those making $50,000 to $99,999, and those making more than $100,000. I call these groups “low-income,” “medium-low-income,” “medium-high-income,” and “high-income,” respectively. With 78 percent of respondents choosing to answer the income question, the sample was reduced to 282,701. Twenty percent of respondents are classified as low-income, 27.6 percent as medium-low-income, 33.6 percent as medium-high-income, and 16.5 percent as high-income. For the 2012 CCES, the boundary defining low and medium-low income is $30,000 instead of $25,000. For the analysis in the main text, I include the 2012 CCES data, but in the appendix I replicate all of the results excuding these data; the results are largely unchanged.
There are 264 unique policy questions in this data set. However, responses to these questions are sparse owing to the fact that different surveys ask different policy questions. Following Tausanovitch and Warshaw (2013), I identify the positions of respondents to different surveys relative to one another by constraining common questions to have the same item parameters.1 In addition, I use smaller sample surveys attached to the large 2010 and 2011 CCES surveys to provide more linking questions. The purpose of these surveys was to ask 177 of the questions that had been asked in prior surveys in order to estimate the item parameters in a common space. Later surveys are linked using these questions and common questions on the CCES. This method for linking large sample surveys and the data for doing so come from Tausanovitch and Warshaw (2013).
Data for the positions of legislators come from Keith Poole and Howard Rosenthal’s DW-NOMINATE scores (Poole and Rosenthal 1997).2 Although the functional form of DW-NOMINATE is different from the Bayesian quadratic item response model outlined here, in practice it results in very similar estimates, and so for convenience I use it here. Rather than respond to survey questions, members of Congress cast roll call votes on policy issues. DW-NOMINATE scores are calculated using members’ roll call votes as their statements of preference. Since these votes are actually yes-or-no choices, they are amenable to a binary model.
In the main analysis, districts are matched to their respective members of the House of Representatives and the Senate for the 111th Congress (2009–2011). The choice of Congress is somewhat arbitrary, because survey data are drawn from a period covering six congressional elections. Using each possible legislator-district pair over this period would be, in a sense, double-counting observations. In the appendix, I rerun the analysis using every Congress from the 106th through the 112th—all of the sessions that used the year 2000 census districts. I comment on important discrepancies between these results and the results reported in the main text where appropriate.
Prior work on this topic focuses on the Senate owing to sample size constraints (Bartels 2009; Bhatti and Erikson 2011). I focus on the House, while replicating my analysis for the Senate. The Senate analysis is more consistent with previous findings. At the same time, greater multicollinearity and fewer legislator observations make the Senate results more uncertain.
The CCES provides district identifiers for each respondent. For the NAES, I match respondents probabilistically to their districts using their zip codes. Most zip codes are fully contained within districts, but where there is partial overlap with multiple districts, the extent of the overlap is used to calculate the probability that a given respondent resides in a given district. Districts are from the year 2000 redistricting.
RESULTS: INCOME AND REPRESENTATION
Is it in fact the case that higher-income voters are better represented than lower-income voters? Although more attention has been given to those arguing in the affirmative, there are some nicely executed counterexamples. Using much larger sample sizes than the original Bartels (2009) study, both Bhatti and Erikson (2011) and Brunner, Ross, and Washington (2013) find mixed evidence of differential representation. Both studies have disadvantages. Bhatti and Erikson (2011) use respondents’ self-placement using abstract ideological labels (“very liberal,” “liberal,” “moderate,” “conservative,” and “very conservative”) as the measure of respondent positions. Brunner, Ross, and Washington (2013) use ballot propositions to measure voter ideology, but there are a limited number of such propositions in each election; in addition, they measure income at the neighborhood level, in California only. Nonetheless, their data come from the universe of voters, and as a result their sample size is enviable. In contrast to these papers, I use a large national sample of individuals responding to large numbers of policy questions, with income measured at the individual level.
Why have existing studies come to different conclusions regarding representation? One explanation is that the variables that we seek to distinguish are highly collinear and measured with error. Table 1 shows the pairwise correlations between five variables in U.S. House districts. μH is the mean preferences of high-income constituents (annual income more than $100,000), μMH is the mean preferences of medium-high-income constituents ($50,000 to $99,999), μML is the mean preferences of medium-low-income constituents ($25,000 to $49,999), and μL is the mean preferences of low-income constituents (less than $25,000). The mean preferences of all constituents is μ. The lowest correlations are between the preferences of low-income constituents and other groups, but all of these correlations are very high. Unlike past studies, these measures reduce error through the use of a measurement model. Nonetheless, all of the quantities are measured with error that is due in part to measurement and in part to sampling. High correlations between each quantity raise the possibility of autocorrelated error, which can cause instability in regression coefficients. Table 2 shows that the corresponding multicollinearity in the Senate is even more problematic.
Pearson Correlations Between Mean Preferences of Income Groups Within Congressional Districts
Pearson Correlations Between Mean Preferences of Income Groups Within States
I begin by replicating the methodology used by Bartels (2009), using the data for the Senate. In each district I calculate the percentage of the sample that falls into each group. I call this pg, where g indexes the group L, ML, MH, and H, respectively. I then decompose the mean preferences of the district into the means of each group, multiplied by the proportion in that group. By Bartels’s logic, if legislators represent mean preferences in their district without regard to income, then the coefficients in a regression of legislator position on the proportion-weighted group means should all be equal. If the coefficient on one group is higher than the others, this is consistent with the hypothesis that legislators change their positions more in response to this group than to the others.
Table 3 shows the results of three regressions for the 111th Senate. The first two are univariate models that simply regress the position of the legislator on the preferences of low-income and high-income people, respectively. The third is the specification from Bartels (2009) that includes each group and weights them by their proportion in the district. The first two models show that both the preferences of the poor and the preferences of the rich are related to legislator positions. However, model 3 is consistent with Bartels’s argument. When each income group is included in the model, multiplied by their proportion in the district, only the preferences of the high-income group are significantly related to the positions of the legislator. The preferences of the rich have a signficantly greater effect than the preferences of the poor, and in fact it appears that the poor have no effect at all. These findings hold regardless of which Congress we examine from the 106th to the 112th, as shown in the appendix.
Regression of Legislator Position on Income Group Preferences in the U.S. Senate
Table 4 shows the same models for the House of Representatives. By Bartels’s criteria, this model refutes the hypothesis that the rich are better represented than the poor in the House. On the contrary, if anything, low-income people appear to be better represented. Not only is the coefficient in model 1 for low-income preferences greater than the coefficient in model 2 for high-income preferences, but in the combined specification the lowest income group has the greatest coefficient. The effects in model 3 have an oddly nonlinear pattern: the poor garner the greatest coefficient, but the medium-low-income group receives a coefficient that is indistinguishable from 0. This is contrary to any expectation from the literature, and to my own expectation. Once again, the appendix shows that the findings of seemingly greater representation of the poor are consistent across sessions of Congress. (The other coefficients vary substantially.) What could explain these results?
Regression of Legislator Position on Income Group Preferences in the U.S. House of Representatives
One possibility is that the proportions of rich and poor constituents are variables that capture the urban/rural split that we observe when we divide districts represented by Democrats from those represented by Republicans. The variance of preferences among the poor is much lower than the variance of preferences among the rich, probably because of greater measurement error in the preferences of the poor. However, the proportion of the poor who cross a threshold of “liberalness” may be a good indicator of an urban district, a poor district, or a majority minority district. Rather than gather detailed district-level data, we can account for this sort of possibility by simply controlling for the proportions of the district sample that are in each income group. Table 5 does just this, replicating each column from table 4 but with controls for the proportion high-, low-, and medium-low-income, with medium-high-income as the excluded category. This specification is similar to the one used by Bhatti and Erikson (2011).
Regressions Explaining Legislator Position in the U.S. House of Representatives, Controlling for Income-Only Variables
The results from table 5 are much more intuitive than the results from table 4, as well as closer to previous findings. Controlling for the income of a district, legislator responsiveness appears to increase with the income of each group. However, these coefficients are not significantly different from one another. Furthermore, the results are not consistent across different sessions of Congress. In the appendix, I show that the results from the 106th and 107th Congresses place greater weight on the middle-income groups and the least weight on the high-income group.
Given the ambiguity of the results in tables 4 and 5, it is too soon to conclude that the poor are dramatically underrepresented in the House of Representatives. Research tends more often than not to find that the poor are underrepresented in the Senate, but studying the House has not generalized this conclusion. However, the coefficients in these regressions are not the only way in which we can conceptualize responsiveness or representation.
The approach taken to examining responsiveness so far assumes that the coefficient on group-level preferences is the best measure of whether legislators are “responding” to voter preferences. It is difficult to know how to interpret this coefficient. Legislator positions and voter positions are measured quite differently, and so a larger coefficient could measure overreactions to constituent preferences as easily as it measures better representation. One simple question we might ask is whether the positions of the poor or the rich are more accurate predictors of legislative positions. If legislators are truly focusing on one group more than the other, then our predictions of legislator positions should be closer to the truth when we use the preferences of the better-represented group as a regressor. The evidence on this question from tables 4 and 5 is clear: the variance explained is always higher using the high-income group than the low-income group. This holds for the Senate as well.
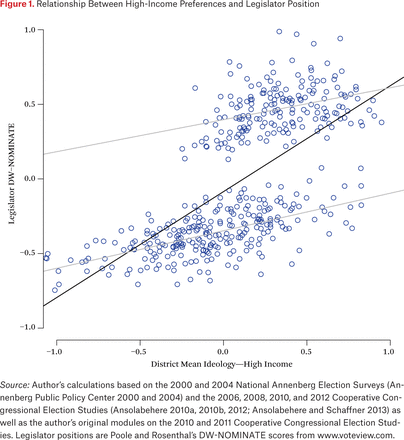
To understand what this means exactly, consider figure 1. This figure graphs the univariate regression line of legislator positions on the positions of high-income constituents, overlaid on the scatterplot of the data, for the House. The gray lines in the figure show the regression lines for Republican legislators only (the top cloud) and Democratic legislators only (the bottom cloud). The reason for showing these regression lines should be clear from the plot. The relationship between legislator and constituent positions is hardly linear. The polarization in legislator positions means that the transition between liberal and conservative legislators is not smooth. In contrast, the positions of high-income constituents are spread relatively smoothly throughout the preference space. The bottom line here is that most of the variance, and hence most of the variance explained, is between-party. Within-party the lines are relatively flat and the variance explained is much less.
Relationship Between High-Income Preferences and Legislator Position
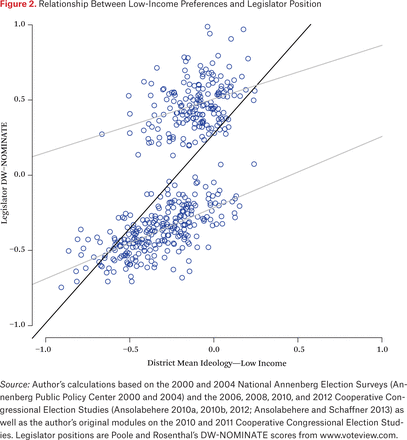
Figure 2 shows the univariate regression line, scatterplot, and associated within-party regression lines when the positions of low-income constituents within districts are used as the explanatory variable. There are two main differences between this plot and the previous one. First of all, the variance explained is lower, both within- and between-party, while the slope of the lines is much steeper. At the same time, the reason for this steeper slope is quite apparent: there is much less variation in terms of positions. Low-income voters are to the left of high-income voters on average, but their estimated positions also tend to be closer to zero. We might expect to find this result if poorer constituents report their policy views with greater error.
Relationship Between Low-Income Preferences and Legislator Position
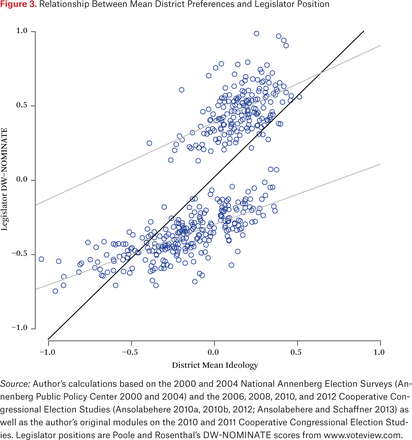
Finally, figure 3 shows what happens when we use the mean for the entire district to explain legislator positions. This variable explains more variance than either of the other two, with an R-squared statistic of 0.51. And yet the key feature of the relationship remains: the variance explained is mostly between-party (not too surprising, since the y variable has not changed), and our ability to explain within-party variance is relatively poor. In fact, figures 1, 2, and 3 are surprisingly similar. The differences in the relationship are overshadowed by the common disjuncture between the distribution of district opinion and the distribution of legislator positions.
Relationship Between Mean District Preferences and Legislator Position
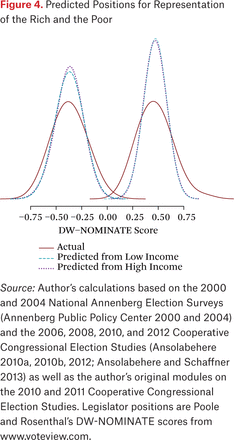
One way to think about the substantive implications of these different relationships is to consider a hypothetical in which legislators do in fact respond only to low-income constituents or only to high-income constituents. We can estimate a univariate model within-party for each group, generate predicted values, and examine which set of predicted values better matches reality. Figure 4 shows the result of this exercise for the House of Representatives, including the distribution of actual legislator positions. The distributions of predicted values in figure 4 are less dispersed than the actual distribution of legislator positions. In contrast, they differ little from each other. This is evidence that noisy representation of all groups is much more significant than differences in representation between people at different income levels. The disparity between the two sets of predictions is hardly noticeable.
Predicted Positions for Representation of the Rich and the Poor
Although this discussion of the role of the distribution of preferences has focused on the House of Representatives, these conclusions apply to the Senate as well, since it also is highly polarized. District mean preferences are a better predictor of legislator positions than the mean for high-income constituents, which is better than the mean for low-income constituents. These results hold within and across parties. Explanatory power within-party never exceeds an R-squared of 0.36.
RESULTS: INCOME AND LEGISLATOR PARTISANSHIP
Figures 1, 2, and 3 show that our ability to explain within-party variation in legislator positions using constituent ideology is limited in the U.S. House. As a result, we might think that a more reasonable model of representation is one in which constituent ideology is responsible for the party of the representative but not the representative’s particular set of policy positions. For our purposes, the question becomes: are high-income people more important in deciding the party of the representative than low-income people?
To test this hypothesis, I adapt the regression models from table 5. Instead of using a linear model in which the dependent variable is the legislator’s position or DW-NOMINATE score, I employ a logistic regression model in which the dependent variable is whether or not the legislator is a Democrat. Districts or states are more likely to be represented by Democrats when the population is more liberal. However, if higher-income people have more importance in determining electoral outcomes, we might expect the preferences of higher-income people to be a more important determinant of the partisanship of representatives.
Table 6 reports the result of a logistic regression model along the same lines as table 5, but using the Senate and with the party of the legislator as the dependent variable. Models 1 and 2 suggest that in states with more conservative citizens, either low-income or high-income, the senator representing that state is less likely to be a Democrat. Model 3 shows that when these income groups are included in the same model, the coefficients for the top three income groups indicate that conservative views lead to less likelihood of Democratic representation. However, the coefficient for the poor is insignificant and substantially in the wrong direction. The greatest coefficient is for the views of high-income constituents, although this difference is not significant. The coefficient on the proportion poor suggests that poorer states are more likely to be represented by Democratic senators, all else equal. These coefficients are unstable across different sessions of the Senate, but the coefficient for the highest-income group is always the greatest in magnitude.
Logistic Regressions Explaining Legislator Party in the U.S. Senate (1 = Democrat)
Table 7 repeats this model specification for the House of Representatives. The first two columns of the table show findings similar to those in table 5. In a model including only the preferences of low-income constituents, the slope of the relationship between the mean preferences of low-income constituents and the probability of electing a Democrat is significant. This relationship is also significant in a model with the mean preferences of high-income constituents as the primary independent variable. The slope of this relationship is significantly less steep, although the model fits somewhat better. In both cases, the relationship is negative, as expected: more conservative constituencies are less likely to elect Democrats.
Logistic Regressions Explaining Legislator Party in the U.S. House of Representatives (1 = Democrat)
The third column of Table 7 shows the model including all covariates. Although in every case the relationship between the preferences of each group and the probability of electing a Democrat has the expected sign, only two of the coefficients are significant. The positions of high-income people have by far the largest slope. The medium-high-income group appears to have the smallest slope, while the low-income and medium-low-income groups are in a close tie for second place. The coefficent on the preferences of the rich is significantly greater than the coefficients on the preferences of the other groups, which are all statistically indistinguishable. However, this result does not hold in the 106th or 107th Congresses. Notably, in all specifications, and in all sessions of Congress, the proportion of the district that is poor has a substantial positive effect on the probability of electing a Democrat.
Coefficients are notoriously difficult to interpret in logistic regression models. A visualization is helpful in understanding the substantive difference between the effects for the rich and the poor. I use a model very similar to the one from the last column of table 7 to show the predicted change in the probability of electing a Democrat based on a change in the ideology of the mean low-income and high-income constituent, respectively. The only difference between the model used to calculate these probabilites and the model in table 7 is that the former includes all direct effects, following the folk wisdom on using interactions in regression models (Brambor, Clark, and Golder 2006). This change in specification makes very little difference in the resulting probabilities. To calculate the change in probability I hold all other variables besides the variable of interest at their mean.
Figure 5 shows the result of this exercise for the House of Representatives. The left panel shows the predicted probability of a Democratic legislator given the preferences of low-income constituents, and the right panel shows the predicted probability of a Democratic legislator given the preferences of high-income constituents. As expected from the regression table, the slope is steeper for high-income constituents. Nonetheless, the slope in the left panel is not flat: Democratic legislators are substantially more likely when poor constituents are liberal than when they are conservative. Note that if we were to examine the 106th or 107th Congresses, the slopes for the preferences of the higher-income group would be flatter, reversing this relationship.
Probability of a Democratic Legislator by Ideology of Income Groups
The “rug” for each graph shows the distribution of the mean constituent preferences. As discussed, the variation in preferences is substantially greater for high-income than low-income constituents. In this case, the range where the slope for high-income constituents exceeds the slope for low-income constituents occurs in a region where there are no data for low-income constituents. Specifically, there are very few districts where the mean ideology of low-income constituents is to the right of zero. In contrast, for high-income constituents, most of the decline in the likelihood of electing a Democrat occurs to the right of zero. Our analysis has told us that the slope is steeper in the right panel, but this steep slope occurs in a region where we have no data in the left panel. In other words, we cannot tell how unlikely the election of a Democrat would be in a district with very conservative poor residents because no such district exists.
CONCLUSION
In this paper, I have shown that while there is some evidence that lower-income people are less represented in Congress, this evidence is robust only in the context of the Senate, not the House of Representatives. Even in the Senate, the substantive importance of this difference is limited in comparison to the gap in overall representation. Given the small extent of differential representation and the uncertainty regarding it, priority should be given to understanding overall representation and the reasons why the distribution of legislator preferences is so different from the distribution of average preferences in districts. Separating the public into large categories by income does not seem to help us solve this puzzle.
To understand how representation is unequal, better theories of representation are needed. A good theory of representation should account for the fact that most of the variance in legislative positions is currently between parties. With such a theory, political scientists would be better able to evaluate whether legislators take the preferences of their constituents into account without regard to income. In this paper, I have used two very basic theories: that legislators represent the mean voter, and that the party of the legislator is determined by the mean voter. Future research should strive to build richer theories of representation from microfoundations.
One possible explanation for the small amount of differential representation that I find is that there is more measurement error in the preferences of the poor than in those of the rich. This would affect the analyis insofar as preferences have been imperfectly observed. However, legislators as well as political scientists may have more difficulty observing these preferences. Future research should investigate this possibility as a cause of the weak representational link.
There is one argument that I have not made in this paper: that low-income people are in fact well represented. Work that makes the argument that the political system does not represent the poor very well may be right. Much depends on a value judgment about what aspect of preferences should be represented. Certainly the political system has not responded to the economic needs of lower-income people in a way that standard political economy models would predict (Bonica et al. 2013; Hacker and Pierson 2011). The findings of this paper may plausibly answer the question posed by Adam Bonica and his colleagues (2013): why hasn’t democracy slowed rising inequality? If legislators respond only weakly to their constituents in general—and perhaps respond especially weakly to their low-income constituents in particular—then not one but two conditions are violated that would be needed to beget a democratic response to rising inequality. Determining which institutions might affect both of these links and examining the downstream effects of doing so are urgent matters for future research.
Acknowledgments
This work builds on work in my dissertation that benefited greatly from comments and feedback from David Brady, Morris Fiorina, Simon Jackman, Jeffrey B. Lewis, and Howard Rosenthal. It also builds on work with Jeffrey Lewis creating the software necessary to estimate the model of preferences. All mistakes remain my own.
FOOTNOTES
↵1. This assumption may not be correct if, for instance, the interpretation of the items changes over time. Although testing this assumption is beyond the scope of this paper, see Lewis and Tausanovitch (2013).
↵2. Data provided at the Voteview website (www.voteview.com, accessed August 2014).
- Copyright © 2016 by Russell Sage Foundation. All rights reserved. Printed in the United States of America. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Reproduction by the United States Government in whole or in part is permitted for any purpose. This work builds on work in my dissertation that benefited greatly from comments and feedback from David Brady, Morris Fiorina, Simon Jackman, Jeffrey B. Lewis, and Howard Rosenthal. It also builds on work with Jeffrey Lewis creating the software necessary to estimate the model of preferences. All mistakes remain my own. Direct correspondence to: Chris Tausanovitch at ctausanovitch{at}ucla.edu, 3383 Bunche Hall, University of California–Los Angeles, CA 90095.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.