Abstract
The Coleman Report argued that family background is a fundamental cause of educational outcomes, while demonstrating the weak predictive power of variation in expenditures and facilities. This paper investigates the effects of family background, expenditures, and the conditions of school facilities for the public high school class of 2004, first sampled in 2002 for the Education Longitudinal Study and then followed up in 2004, 2006, and 2012. The results demonstrate that expenditures and related school inputs have very weak associations not only with test scores in the sophomore and senior years of high school but also with high school graduation and subsequent college entry. Only for postsecondary educational attainment do we find any meaningful predictive power for expenditures, and here half of the association can be adjusted away by school-level differences in average family background. Altogether, expenditures and facilities have much smaller associations with secondary and postsecondary outcomes than many scholars and policy advocates assume. The overall conclusion of the Coleman Report—that family background is far and away the most important determinant of educational achievement and attainment—is as convincing today as it was fifty years ago.
In Equality of Educational Opportunity (EEO), James S. Coleman and his colleagues offered empirical results that continue to shape our understanding of schooling five decades later. Yet the structure of inequality has not stood still since the Coleman Report was published in 1966. In the interim, we have seen a growth of labor market inequality, including a soaring college–to–high school wage premium, and now a related explosion of wealth inequality. Both developments have altered the resource distribution available to educate new cohorts of children, and some evidence now exists that gaps in educational achievement have grown between the rich and the poor. At the same time, the intense concern with racial differences, which was the axis of inequality that gave rise to EEO, has receded somewhat, even though most of the differences considered then remain distressingly large now. Finally, changing patterns of family formation and immigration have created new patterns of racial differences in educational outcomes, demanding more refined analysis than can be motivated by templates from the past.
Atop this shifting terrain, the conclusion of EEO that was immediately most controversial remains in a similar position. Many scholars and policy advocates accept the conclusion that school expenditures and other inputs that are comparatively easy to change do not determine educational outcomes to a substantial degree (see, for example, Hanushek 1994, 1996, 2001). Other scholars and alternative policy advocates continue to doubt this primary conclusion, as well as most of the research that has generated more recent support for it, and rely on arguments first constructed in the 1960s and 1970s (for example, Baker 2012). These counterarguments are typically based on two primary claims. First, school expenditures and facilities measured at aggregate levels do not closely map onto the schooling inputs delivered to individual pupils. As a result, measures of district-level characteristics cannot, by their very nature, compete effectively for explanatory power with family background measures that reflect the circumstances of each student.1 Second, even if such measurement concerns could be addressed comprehensively through a granular accounting of inputs into each classroom in the nation, statistical models estimated with observational data cannot deliver clear results on relative impact. Regression adjustments cannot solve the identification challenge produced by an empirical regularity known all too well: pupils who attend schools with the best facilities are the same pupils most advantaged in the home.2
Both sides in this debate can claim, without too much hyperbole, that policy has responded to their conclusions. The accountability movement, which culminated in and may well have been destroyed by the No Child Left Behind legislation, is consistent with the position that it is school management and school performance, not school resources and facilities, that must be fixed (see Hanushek and Jorgenson 1996). The accountability movement’s recent transmutation into a campaign to incentivize teacher effectiveness is supported by the same arguments, ratcheted down from school performance to classroom performance (see Hanushek and Lindseth 2009).
Yet policy responsiveness has not been all on the side of the education reform movement. A corresponding movement to narrow resource and input differentials can also claim many victories, often in response to court rulings that have prompted state legislatures to act to ensure higher levels of base funding for schools, through so-called foundation programs. The success of this funding movement, which began before most observers date the successes of the accountability movement, has expanded the amount of funding from state tax revenue that is delivered to local school districts, complementing the growth of federal spending.3 Many courts have now accepted the position that schools with the most disadvantaged students must be provided with substantially more resources than other schools in order to give their pupils a fair shot, through an adequate education, to meet the standards promulgated in legislative responses to the accountability movement (see Baker and Green 2009; West and Peterson 2007). State legislatures have been slow to implement policies in recognition of this new wave of funding decisions, but we may see new increases now that states are no longer able to delay the implementation of remedies because of weak tax revenues in the wake of the Great Recession.
The net result of all of this scholarly contestation and policy change has been a changing set of standards and inputs into schools. School resource differences across particular districts and schools have fluctuated over time (see Corcoran and Evans 2015), but overall levels of resources have increased substantially. At the same time, the monitoring of students, teachers, and school performance is more intrusive than ever. It is reasonable to wonder, therefore, whether the claim that resources and inputs appear to matter surprisingly little has more or less support than in the past. And it is of particular importance if empirical support is accumulating that differences in educational outcomes are growing between the children of the rich and the children of the poor.
RECONSIDERATION OF THE EEO CONCLUSIONS
Initial replications of the EEO results, using what data were available in the years following its publication, were largely supportive of the claim that family background is vastly more important than school resources and facilities (see Jencks 1972, Smith 1972, and other chapters in Mosteller and Moynihan 1972a). Because the literature from the 1980s and 1990s did not substantially alter the support for the EEO conclusions, overview pieces in sociology that have reflected on the report have typically interpreted its conclusions as valid, while then considering the vast literature that has accumulated since its publication to document plausible mechanisms for the overwhelming predictive power of basic family background measures (see, for example, Gamoran 2001; Gamoran and Long 2007; Sørensen and Morgan 2000). Among the lines of scholarship that are particularly valuable for explaining within-school variance, which was perhaps first highlighted most carefully by Frederick Mosteller and Daniel Patrick Moynihan (1972b), a large literature has emerged to explain how effectively, and sometimes unjustly, public schools sort students into structural positions that either support or undermine their life prospects by distributing opportunities for learning differentially. The literature on curriculum tracks alone runs to hundreds of articles, chapters, and books.
Perhaps unsurprisingly, sociologists of education, who are the group of social scientists most heavily influenced by Coleman, have not given much attention to differences in expenditures and facilities in recent decades. This territory has been dominated by a different breed of social scientist: economists and school of education faculty who specialize in educational finance. Much of the conventional wisdom of this subfield is available in Ladd and Goertz (2015), where it can be seen that many of the same debates of the past live on, although at a much higher level of sophistication. (For example, compare Burtless 1996 and Ladd, Hansen, and National Research Council 1999 to Ladd and Goertz 2015.) Working sometimes as consultants in court cases and to state legislatures, some of these scholars have participated in the development of new funding formulas for real-world implementation.
Among the most recent attempts to reconsider the EEO conclusions, the results are a bit more variegated, leaving scholars such as Bruce Baker (2012) some scope to attempt to argue that school resources do matter a lot and always have. Norton Grubb (2009), through a book-length treatment analyzing the high school class of 1992 but using data from the eighth grade in 1988 through follow-ups stretching to 2000, shows that standard measures of expenditures continue to have weak associations with school outcomes, as in EEO. While developing this result, Grubb also asserts that school differences in practices and policies, such as the prevalence of curriculum tracking and innovative teaching, should be labeled school resources as well. And because these sorts of school resources have far more predictive power than dollar-denominated financial resources, he argues that his properly broad conception of school resources demonstrates that school resources matter a great deal. In particular, he writes, “Overall, these results firmly reject the simplistic notion that schools don’t make a difference. School resources increase the explanatory power more than any other set of variables” (Grubb 2009, 69).4
Geoffrey Borman and Maritza Dowling (2010) reanalyzed a subset of the original EEO data, although without the crucial direct measure of expenditures from EEO that is no longer available. With a full deployment of multilevel models developed two decades after EEO was written, they make the case that between-school differences in the test performance of high school students are larger than was recognized for the original analysis as well as for the early replications, such as Jencks (1972) and Smith (1972). Still, Borman and Dowling do not substantially challenge the original conclusions, even though other scholars, such as Baker (2012), interpret their piece as claiming otherwise.5
Finally, not all sociologists have left the core controversy to economists and their colleagues in education schools. Jennifer Jennings and her colleagues (2015) have developed the case for an old counterargument to the possibly apocryphal “all family” conclusion of EEO. They argue that the effects of schools—and presumably resources and related inputs—are much stronger for levels of educational attainment than for performance assessed by standardized tests given in high school. This argument is most common in efforts to modify conclusions on the apparently weak effects of desegregation remedies, where short-run associations are downplayed in light of long-run benefits (see, for example, Wells and Crain 1994), but the argument is also present in the core controversy over the effects of resources (see Card and Krueger 1992, 1996).
If there is a consensus position now among that group of scholars not prone to over-interpretation, it is a decidedly begrudging one. Neighborhoods, families, schools, and diverse environments are all thought to matter, and resource inputs to schools can matter. Many articles take such a nested-spheres-of-influence approach to support the first point (for example, Altonji and Mansfield 2011). But it is the second point that is supported by perhaps the best four-page book chapter written in the field, which is the account by Richard Murnane and Frank Levy (1996) of a modest intervention in Austin, Texas, to boost resources and which shows how money can matter, but often does not.6 And this is perhaps where the debate now stands, as shown in review pieces such as Plecki and Castaneda (2009): interventions to increase funding and resources can matter, and the task of future research is to determine when and how this can be made to be the case more frequently. With this fragile peace, the debate on policy reform can be continued, with the battle lines drawn between those who advocate for increased funding without substantial reforms and those who advocate for reforms to make existing funding matter more.
Although we have no fundamental objections to this consensus opinion, it does leave, we think, important empirical questions on the table, and ones that ought to be answered in a collection of papers that celebrate the enduring value of EEO. What the consensus does not resolve is whether an analysis, fashioned much as in the original work but taking advantage of the data now at our disposal, would still show weak associations between expenditures and outcomes. A resolution cannot be found in reanalyses of the 1965 EEO data (such as Borman and Dowling 2010); in convincing studies that demonstrate that recent school effects, whatever their source, are larger for educational attainment than for test performance (for example, Jennings et al. 2015); in quasi-experimental assessments of state-adjusted studies that cannot cleanly separate changes in financing from other aspects of reform that occurred at the same time (Card and Krueger 1992; Nguyen-Hoang and Yinger 2014); or in innovative studies that are nonetheless geographically limited and lack information on students and their families beyond recorded eligibility for free and reduced-price lunch (Archibald 2006).
What we offer in this paper is a more deliberate approach to the analysis of the data at our disposal, casting aside the false claim that Coleman and his colleagues were primitive analysts whose work would not pass peer review in our current journals. In the empirical analysis to follow, we address two unabashedly EEO-style questions:
Across a categorization of race-ethnicity that can motivate an assessment of educational opportunity in 2015, what are the disparities in resources and facilities across regular public high schools in the United States?
Can these disparities account for differences in educational outcomes, measured during and after high school, or is it still the case, as in EEO, that family background appears to be of preeminent importance?
Although these questions are familiar, we have better data than ever before, and more perspective on what established methods can deliver.
DATA
For our analysis, data for students and their parents are drawn from the Education Longitudinal Study (ELS), 2002 to 2012. The base-year ELS sample is representative of all tenth-grade students in the United States enrolled in public and private schools in the spring of 2002. Additional school-level and district-level data, sourced from the Common Core of Data (CCD) for the 2000–2001 through 2003–2004 school years, were matched to the ELS data records, with the years for the match chosen to correspond to the four years in which the modal ELS student was enrolled in high school. (Note, as already implied by our two questions, that we will not be utilizing a data source that contains information on school differences before the tenth grade. We discuss the implications of this restriction in the discussion section.)
Analytic Sample
Among the original 2002 base-year ELS students, 84 percent participated in the 2012 third follow-up survey. Our models include the respondents for whom third follow-up educational attainment data are available, weighted to adjust for base-year participation, attrition across the waves, and item-specific nonresponse for educational attainment.
We exclude some additional students based on their schools. First, we exclude all students sampled in private high schools because the focus of this paper is the legacy of EEO for K–12 public schooling (and because we have no data on the finances of private schools with which to mount an analysis). Second, we exclude students in four public schools that did not have valid school finance data in the CCD. Third, following our own first-stage data quality assessment, we decided to exclude students in four additional public schools. One of these schools, we believe, was mistakenly included in the sample universe and should have been ruled out of scope.7 The other three schools had what we regarded as implausible data for per-pupil expenditures from the CCD. Students from the first of this latter group of excluded public high schools were simply struck from the sample, since our retrospective decision was that they were not part of the universe of interest, as defined by the National Center for Education Statistics (NCES). Students from the other seven excluded public schools were dropped from the core analytic sample on which models of inputs and outcomes are based, but because they were part of the universe, they were retained for the construction of the analytic weight and made part of the underlying ratio adjustment for participation in the full panel sample. Our resulting weight therefore generalizes the results to these students as well.
With these school exclusions, our analytic sample is composed of 8,037 students, attending 559 regular public high schools. When weighted, the analytic sample is representative of all sophomores in public high schools for the universe selected by NCES, which excludes high schools that cater solely to vocational education students or special needs students.
Measures
Our outcome variables are standardized tests in reading (tenth grade in 2002) and mathematics (tenth grade in 2002 and two years later in 2004), on-time high school graduation in 2004, enrollment in any type of postsecondary education at any point between 2004 and 2012, and receipt of a bachelor’s degree by 2012. We utilize family background measures constructed from responses to the parent questionnaires, which were completed by 85 percent of students’ parents or legal guardians. When missing, we utilize available reports from the students’ questionnaires and regression imputation for a small number of cases. The school survey administrator questionnaire yields ratings of school facilities, and the CCD supplies the student racial composition of each school as well as finance data at the district level. We introduce the details of particular measures in the course of presenting the results.
RESULTS
Racial Segregation in the ELS
What is the pattern of racial segregation in ELS schools? Table 1 presents a cross-tabulation of racial segregation where the eight rows represent a reductive, yet reasonable, categorization of self-identified race-ethnicity, as well as one embedded dimension of ancestry. It is the primary categorization of interest at the time of EEO, but now tuned to engage the growing interest in the educational prospects of the different types of students who claim Mexican ancestry.8 (For readers interested in a less reductive categorization, we offer elaborated tables with twenty categories in supplementary appendix tables S1–S4. For readers interested in a broader discussion of segregation, see Sean Reardon’s contribution to this issue.) The columns of the cross-tabulation are then the percentage of each student’s school that is designated either “black/African American” or “Hispanic,” calculated from the administrative reporting encoded in the school universe files of the CCD.
Racial Composition of ELS High Schools by Respondents’ Self-Identified Race-Ethnicity and Immigrant Generational Status If Claiming Mexican Ancestry
Subject to some measurement qualifications to be discussed later, table 1 reveals pronounced but unsurprising racial segregation. White non-Hispanic students attended high schools that on average were only 9.3 percent black and 6.3 percent Hispanic.9 Asian students, who were disproportionately enrolled in urban schools and in the West, attended schools that were slightly more diverse: 13.7 percent of students were black, and 15.8 percent were Hispanic. In contrast, black students attended high schools that on average were 47.2 percent black, while Hispanic students attended high schools that on average were between 36 and 58 percent Hispanic (varying across the categories in the fourth through seventh rows of table 1).
Because of the importance of these patterns and their role in debates over the implications of EEO, we need to offer additional details of measurement. All ELS students who began the race-ethnicity battery of questions by self-identifying as “Hispanic or Latino/Latina” were then asked their ancestry. Those who selected “Mexican, Mexican American, or Chicano” were allocated to three immigrant generation groups, based on parental and student nativity as well as immigration history. Full details of the coding of immigrant generation are available in Morgan and Gelbgiser (2014). In brief, first- and 1.5th-generation immigrants are those born outside of the United States, with first versus 1.5th irrelevant for this paper but based on the age at which the student entered the United States. Second-generation immigrants are those who were born in the United States and have at least one parent born outside of the United States. Third-plus-generation immigrants are those who were born in the United States and whose parents were born in the United States as well. Finally, self-identified Hispanics who did not select the ancestry of “Mexican, Mexican American, or Chicano” were placed in a fourth group composed of seven separate ancestry groups, with no distinction made by immigrant generation, largely because of sample size constraints (see supplementary appendix table S1).
ELS students who did not self-identify as “Hispanic or Latino/Latina” were categorized by self-reported racial identity and sorted into the remaining categories in table 1, which, for the sake of brevity, we typically characterize in the text of this paper as white, black, Asian, and American Indian.10 None of these groups are sorted by immigrant generation, and they are all reductive in ways that hide important variation in self-identification and lived experiences. Furthermore, it should be kept in mind, when interpreting the results that follow, that Hispanic self-identification receives coding dominance. Thus, all four groups of Hispanic respondents include heterogeneity in self-identified race, including a substantial number of respondents who selected “Black/African American” for racial self-identification.11
The percentages defined for the two columns of table 1 are simpler, based on each school district’s counting of the number of students in each ELS high school, designated for reporting purposes as “black” or “Hispanic,” and then as compiled and adjusted by NCES for dissemination through the CCD. According to the documentation for the data source, the category of “black” is meant to be used for black or African American non-Hispanic students, which aligns with our choice of coding dominance for Hispanic ethnicity with the ELS data. However, it is unclear how well schools and their controlling agencies effectively sorted their own pupils into the same categories that their students would have chosen if given the opportunity that ELS respondents received.
Equality of Opportunity and Inequality of Outcomes
As Coleman explained long ago, a pronounced shift occurred in the latter half of the twentieth century toward a conceptualization of equality of opportunity reliant on measurable equality of outcomes, not simply equality of inputs (see Coleman 1968/1990). This shift has continued, and it now constitutes the most important rationale for the adequacy movement. Table 2 presents mean differences in six measures of educational outcomes available for ELS students.
Standardized Test Results and Subsequent Patterns of Educational Attainment for Groups Defined by Race-Ethnicity and Immigrant Generational Status If Claiming Mexican Ancestry
With white non-Hispanic students as the largest group, and serving as the traditional baseline against which other groups are compared, gaps in test scores are substantial. For tenth-grade reading test scores, for example, the black-white achievement gap is 0.8 standard deviations ([32.19 − 24.30]/9.77). For the math tests, the analogous gaps are 0.9 standard deviations in both the tenth grade and two years later. For another important between-group comparison, note that first- and 1.5th-generation Mexican immigrant students had the lowest test scores among all groups for all of the tests.
For educational attainment patterns, similar gaps are present. These differences are particularly large for receipt of a bachelor’s degree by 2012 (eight years after modal high school graduation). The rate of bachelor’s degree attainment was more than twice as high for white and Asian students in comparison to black students and all four groups of Hispanic students.
As with the clarification of categories for table 1, we need to offer one clarification of the outcome distributions for table 2. Recognizing the substantial recent attention to the dropout “crisis,” we note that the corresponding result in the last row of the table may be surprising. The column for on-time high school graduation reveals that 87 percent of ELS respondents graduated from high school on time in 2004, which is high relative to the rates that others have reported based on other data sources. Recall, however, that the ELS is a sample of high school sophomores, and it includes only those who were enrolled in the spring of their sophomore year, when the ELS survey was fielded. Students who dropped out of school before the administration of the survey are therefore out of the universe of the survey, and we know from other research that a substantial proportion of dropouts leave school before the spring of the sophomore year. An important implication of this pattern should be noted now: the school effects analysis that we offer here is relevant only to a subset of students who entered high school at the beginning of ninth grade. Thus, as we discuss in the concluding section, it is possible that the sophomore-and-beyond universe of the ELS robs schools and their characteristics of some of their total effects.
Group Differences in Inputs and Conditions
Table 3 presents group differences in the basic staffing and financial profiles of the 559 ELS schools. In comparison to all other groups, students who claimed Mexican ancestry attended schools that had the highest pupil-teacher ratios and were staffed by teachers with lower levels of advanced educational certification. These students also attended schools with the highest rates of eligibility for free and reduced-price lunch. Black and American Indian students, however, had slightly higher percentages of expenditures from federal sources, which we explain further when we consider the size and composition of total expenditures.
Staffing and Funding Profile by Race-Ethnicity and Immigrant Generational Status If Claiming Mexican Ancestry
Table 4 presents group differences in scores on standardized scales of the conditions and maintenance of school facilities, constructed from factor models of underlying items. The first column presents mean differences for the classroom scale, which is a standard factor-weighted composite of items recorded by the ELS survey administrator for each school:
The classroom ceiling was in disrepair.
Graffiti was present on the classroom walls, ceilings, or doors.
Graffiti was present on classroom desks.
Trash was observed on the classroom floor.
The trash can was overflowing.
Bars were present on classroom windows.
Classroom windows were broken.
Means of Factor-Scored Scales of Poor Conditions and Maintenance of Facilities by Race-Ethnicity and Immigrant Generational Status If Claiming Mexican Ancestry
The scale for hallways is based on seven similar items for the school’s front hallway, noting the presence of trash, graffiti, broken lights, chipped paint, or damaged ceilings. The scale for bathrooms is based on five items: four for graffiti and trash, and one for whether students loiter in the bathrooms while others are in class. The scale for the area outside of the school is based on five items: one for trash, one for graffiti, one for the presence of boarded-up buildings in the area around the school, and two for the preponderance of students and nonstudents loitering around the area of the school.
These scales of conditions, maintenance, and general disorganization follow expected patterns, although with some interesting variation that we surmise is produced by differences partly attributable to the locations of some schools in distressed urban areas. In general, and subject to some variation that is probably attributable to sampling, the highest values for poor conditions and maintenance are present for the schools attended by black and Hispanic students of all types, with white students, Asian students, and American Indian students attending schools with more favorable physical conditions measured by these scales. Because of the composites’ factor scaling, the group differences have no natural metric interpretation. However, the range of variation across groups is generally within one-half of a standard deviation of the full range of variation for each scale (because each is a standardized scale). What is not reported, but is noteworthy, are the within-group patterns of variation. The standard deviations of the four scales are substantially higher among black and Hispanic students, relative to white non-Hispanic students.12 As such, the mean differences reported in table 4 do not reveal the scale of the differences that are present for some of the schools with particularly poor conditions and maintenance.
Table 5 presents group differences in the focal input of interest—expenditures at the district level, as matched to each ELS high school. The first two columns present total expenditures, the middle two columns present expenditures for instructional purposes only, and the last two columns present expenditures for the salaries of instructional staff only.13 All expenditures are averaged over four years of data from 2000–2001 through 2003–2004, which are the four years of high school for a continuously enrolled ELS student. The four-year averages also smooth out year-to-year variation, which may be accentuated by the scale modifications produced by the pupil divisor and the cost adjustment operation discussed later.14
Means of Per-Pupil Expenditures by Race-Ethnicity and Immigrant Generational Status If Claiming Mexican Ancestry
Consider first the raw per-pupil levels of expenditures, ignoring cost adjustments. In contrast to the scales for poor conditions, table 5 reveals in its group differences some patterns that would be quite surprising to readers unaware of debates on school resource levels. For example, for all three measures of expenditures, the levels are higher for schools attended by black non-Hispanic students than for those attended by white non-Hispanic students. The lowest levels are for Hispanic students who claim Mexican ancestry, and the highest levels are for Hispanic students who do not claim Mexican ancestry. As is well documented (see Ladd and Goertz 2015), these differences are produced by a complex set of underlying determinants, the two most important of which are (1) the availability of compensatory funding from federal and state sources for students in poverty and those with special needs, and (2) the higher teacher salaries and other expenses typical of schooling in metropolitan areas, especially in high-wage states, relative to rural areas and all areas in low-wage states.
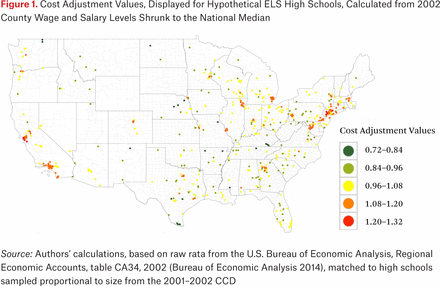
Inspired by some recent approaches in the literature to adjust for the different costs faced by school districts (see Duncombe, Nguyen-Hoang, and Yinger 2015), we constructed a set of cost adjustment values from the average wage and salary levels of jobs at the county level, calculated by the U.S. Bureau of Economic Analysis for the years 2001 through 2004. Because these county-level wage and salary averages are too dispersed relative to public-sector wages, we shrunk the county wage levels toward the national median using an exponential shrinkage parameter, after which we rescaled the wage and salary levels to a proportional adjustment factor with a mean of 1.
To give a sense of the calculated cost adjustment values, figure 1 presents a hypothetical set of ELS high schools, plotted at their actual physical locations but sampled at random (proportional to size) from the 2001–2002 CCD.15 Schools are colored by a weather severity scale, from green through yellow to red, for the size of the cost adjustment value. In particular, the values were binned into five colors for interpretability, as shown in the figure’s legend, but the underlying values used for the analysis vary continuously from 0.72 to 1.32.16
Cost Adjustment Values, Displayed for Hypothetical ELS High Schools, Calculated from 2002 County Wage and Salary Levels Shrunk to the National Median
When nominal expenditures are divided by these cost adjustment values, the effect is to render $13,000 per pupil in red high schools equivalent to approximately $10,000 per pupil in yellow high schools and approximately $7,000 in dark green high schools. At the risk of oversimplifying, the adjustment eliminates expenditure differences attributable to cost differences across high schools in high-wage metropolitan areas like New York City (colored red in figure 1), average-wage metropolitan areas like Toledo (colored yellow in figure 1), and low-wage counties like those in Appalachian Kentucky (colored dark green in figure 1). As we discuss later, this cost adjustment procedure is imprecise and surely inaccurate for many areas, and yet we argue that the adjustment is sufficient to demonstrate how little such cost differences matter for the sorts of models we offer.
To see some of the consequences of our cost adjustment procedures for the expenditures of actual ELS schools, consider the second, fourth, and sixth columns of table 5. After cost adjustments, expenditure differences across groups narrow slightly, with the largest changes being the relative declines in the amount of money spent on the schools attended by non-Hispanic black students (who are more likely to attend urban schools) as well as those attended by Asian students and Hispanic students who do not claim Mexican ancestry (two groups more likely to attend schools in high-wage counties, especially in California and the New York metropolitan area). The expenditure gap between white and black non-Hispanic students is no longer upside down relative to journalistic expectations. The expenditures for Hispanic students who claim Mexican ancestry remain substantially lower than for all other groups.
School Inputs and Family Background as Predictors
Since the publication of EEO, we have had five decades of methodological improvement, yielding many new techniques, as well as a much deeper understanding of the techniques utilized by Coleman and his colleagues. Even so, techniques have not changed so much that it is no longer appropriate to offer an analysis of predictive power by first estimating simple models of the variance explained. Accordingly, table 6 presents estimates of the variance accounted for by predictor variables in ninety different specifications (fifteen each across the same six educational outcomes presented in table 2). For the three test scores, the models are generic ordinary least squares (OLS) regression models. For the three educational transitions models, they are corresponding logistic regression models.
Consider first the models reported in the first three columns for test scores as the outcome variables. Each row of table 6 specifies the predictor variables for each underlying regression model, without any attempts to fashion tighter fits through variable transformations and without any cross-product interaction terms. Just as important, no attempt is made to remove confounding from any “causally prior” variables. Accordingly, all of these models would be regarded as “naive” models in the modern literature on causal inference. With less pejorative labeling from the era of EEO, they would be labeled bivariate or unadjusted regression models.
Proportion of Variance Explained for Separate Naive Linear Regression and Logistic Regression Models, Without Any Adjustments for Confounding and with No Effort to Respecify for Any Suspected Nonlinearities
The specifications are divided into four groups. The first two specifications are labeled “individual” because all predictors are indisputably individual and family characteristics. Consider the first model for the prediction of tenth-grade reading test scores. The eight dummy variables, representing the nine rows used already in tables 1 through 5 for race-ethnicity and immigrant generation, account for 13.6 percent of the variance of reading test scores. The next row is for a model that specifies six variables for family background—mother’s education, father’s education, mother’s occupational standing, father’s occupational standing, family income, and living only with one’s mother or a female legal guardian. These variables account for 17.5 percent of the variance of tenth-grade reading test scores. Now, looking across the first three columns, there is some small variation in the predictive power across all three test scores, but not enough to merit a detailed accounting.
Consider the second group of specifications, labeled “individual and school.” The variables for all four specifications here are characteristics that cannot be cleanly delineated as either individual or school characteristics. The first specification, which includes eleven dummies to parameterize differences across four regions (West, South, Northeast, and Midwest) crossed by urbanicity (rural, urban, suburban), accounts for between 3 and 4 percent of the variance of test scores.17 The racial composition of schools is measured at the school level, but of course these values are based on individual characteristics, with the compositions shaped themselves to a large extent by the residential decisions of parents and the constraints upon them. Thus, racial composition, which can account for between 8 and 10 percent of the variance of test scores, is not clearly a school-level characteristic either.
This “levels” ambiguity is clearest for the final two specifications—the percentage of a school’s students who are eligible for free or reduced-priced lunch and the percentage of a school’s funding from federal sources. Each is nominally a school-level measure, but both are based entirely on family background differences across schools, when measured through administrative rules for transfer allocations for compensatory education programs. The percentage of students who qualify for free and reduced-price lunch can account for 10 to 11 percent of the variance of test scores, while the percentage of funding from federal sources can account for 4 to 6 percent of the variance of test scores.
The next group of specifications are for measured characteristics of schools that are much more clearly attributes of schools themselves. First, two variables for the teaching corps of each school—the level of staffing, summarized by the pupil-to-teacher ratio, and the level of advanced educational certification—can account for only about 1 percent of the variance of test scores. The four conditions and maintenance scales presented earlier can account for about 2 percent of the variance of test scores, matching the results of Alex Bowers and Angela Urick (2011), who develop conclusions based on a similar analysis of the predictive power of these items for the ELS data. And finally, a third specification, which is a scale of items reported by the school principal, labeled as a scale for learning “hindered by” poor conditions and facilities, can account for only 1 percent or less of the variance of test scores.18
The final group of specifications includes district-level expenditure measures, presented earlier in the six columns of table 5. All of these expenditure measures can account for less than 1 percent of the variance of test scores. Contrary to the expectations of some, focusing on instructional resources only, or even more narrowly on the salaries of instructional staff, does not alter the results much at all. Likewise, adjusting for cost differences, as explained earlier for table 5 and as depicted in figure 1, does not change the results either.
The literature has long recognized that the intradistrict allocation of expenditures across schools is not uniform, given both the indivisibility of salary lines and the operation of specialized programs, some for students with special needs and some for students now labeled “gifted and talented.” The ELS, when supplemented by a match from the CCD, does not allow us to examine the importance of these patterns. We can, nonetheless, dispel one concern. When we drop 18 students in charter high schools and 571 students in magnet high schools from the analysis sample of 8,037 students and then reestimate table 6, the results are nearly identical. It is not the case that the 589 students in these schools represent outliers exerting leverage on the estimated regression line that represents the variance explained (as would be the case if students in these high schools all had high performance but comparatively low district-level expenditures that hide higher but unobserved school-specific expenditures).
Now we consider the last three columns of table 6 for models that predict educational transitions. For these models, the notion of variance explained must shift a bit in recognition of the dichotomous outcomes. However, estimation itself is simple, and accordingly we estimate logit models for the outcomes using the same specifications of predictors for the models that predict test scores. In the final three columns of table 6, we offer a measure of the proportion of the variance explained, following the recommendation of Tue Tjur (2009) to compute the difference in predicted probabilities from the model across the two realized values of the outcome. This coefficient of discrimination is a generalization of classification summary statistics, and it is easy to justify as a direct analog to the variance explained in least squares regression.19
The pattern for educational transitions differs in some respects from the pattern for test scores. With the shift to dichotomous outcomes (and with different base rates as well), it may feel unnatural to compare the raw values for the variance explained using Tjur’s (2009) coefficient of discrimination, and so we will spare the reader. Regardless, for the educational transitions, relative comparisons within columns are easily justified, and these relative comparisons can be considered across rows.
For educational transitions, family background accounts for much more variation than our representation of race-ethnicity and immigrant generation. Likewise, free and reduced-price lunch accounts for more variation than racial composition. For all of the models in the school- and district-level specifications, the models have little predictive power, approaching at most 1 percent of the variation for bachelor’s degree attainment. Here, one interpretive complication arises. With variation in unconditional rates for each of the three transitions, the functional form of the logit makes between-outcome comparisons difficult. Partly for this reason, we offer school-level models of attainment rates in table 7 and make the case that expenditures may matter most for bachelor’s degree attainment. Nonetheless, the overall conclusion of this section is unaffected by the complications of between-model comparisons. For all of the models in table 6, expenditures are much weaker predictors of the six outcomes than are measures of family background.
Metric Coefficients for Expenditure Variables for Separate Between-School Models of Tenth-Grade Math Test Scores, With and Without Adjustments for Family Background, Region, and Urbanicity
A Graphical Explanation of Differences in Predictive Power
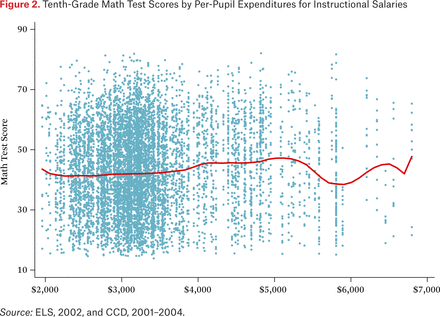
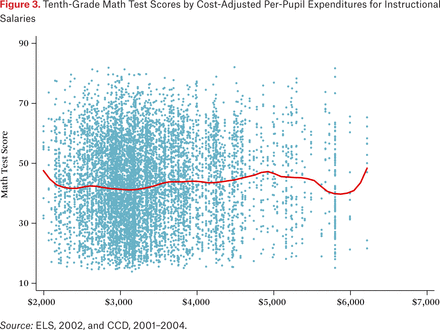
Although the weak predictive power of school expenditures may not be surprising to those who have followed school resource debates, it is still important to explain the “why” and “how” of these results. As a first step, consider figures 2 and 3, which present two scatterplots in which the vertical axis is the math test score in the tenth grade and the horizontal axes are per-pupil salary expenditures and cost-adjusted per-pupil salary expenditures, respectively, in the two figures. Each blue dot is a student, and the red line is a locally smoothed average for the relationship between test scores and salary expenditures.20
Tenth-Grade Math Test Scores by Per-Pupil Expenditures for Instructional Salaries
Tenth-Grade Math Test Scores by Cost-Adjusted Per-Pupil Expenditures for Instructional Salaries
The vast majority of the variation in test scores appears to be within schools, as shown by the wide variation in test results within each school (that is, each vertical line of blue dots is a single school, since per-pupil expenditures nearly always differ just a little bit from school to school). Figures 2 and 3 appear quite similar, suggesting that rearrangements of the ordering on the horizontal axis to take account of costs are unlikely to matter much for the association. The nonparametric smooth presented as the red line fluctuates at its ends, but largely because these are the regions where the data are sparse. If we engage in some unabashed curve fitting, trimming to the interior range from $2,500 to $4,750, we can generate very slightly more predictive power for expenditures (see our between-school models in table 7). Of course, with similar tweaking for other sets of predictors, we could boost their predictive power as well, and it would be hard to know when to stop. The supplementary appendix provides analogous figures for the other five outcomes (see figures S2, S4, S6, S8, and S10). Only the figure for bachelor’s degree receipts suggests a slightly stronger association, as we discuss later.
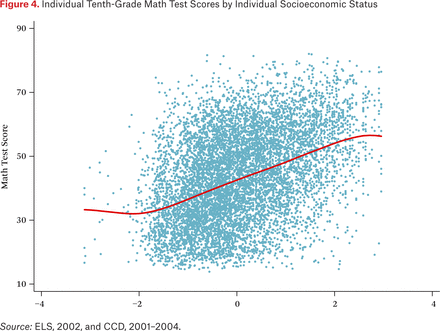
Now we consider the strong predictive power of family background. For figures 4 through 6, we first created a factor-scored variable for socioeconomic status, which is a standardized composite variable for five underlying items (mother’s and father’s educational attainment and occupational standing, as well as total family income). For figure 4, socioeconomic status is the variable for the horizontal axis and the tenth-grade math test score is again the variable for the vertical axis. The red line is an analogous local average line, but unlike for expenditures, it now moves relentlessly upward with increases in socioeconomic status.
Individual Tenth-Grade Math Test Scores by Individual Socioeconomic Status
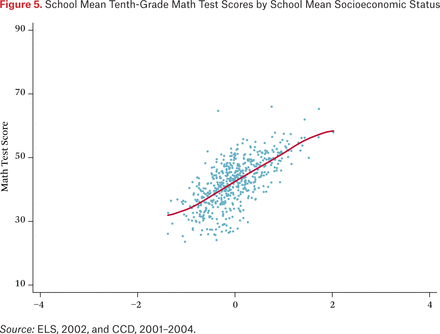
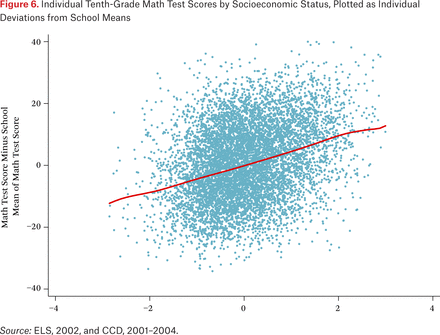
Figure 5 plots the school math test means against the school socioeconomic status means, and figure 6 plots within-school deviations from these mean values for both variables. Figure 5 is hardly surprising, since it is well known that schools with the most disadvantaged students have the lowest observed levels test performance. Figure 6 shows that the within-school relationship between socioeconomic status and test scores is nearly as strong as the total association shown in figure 4. Accordingly, the within-school variation revealed in figures 2 and 3 is not idiosyncratic variation in test performance; a large portion of it is patterned variation that can be predicted by family background. Thus, the overall relationship between socioeconomic status and test scores has important between-school and within-school components.
School Mean Tenth-Grade Math Test Scores by School Mean Socioeconomic Status
Individual Tenth-Grade Math Test Scores by Socioeconomic Status, Plotted as Individual Deviations from School Means
Simple Models with Adjustments
Although measurement debates followed the release of EEO, the most withering criticism was based on the modeling assumptions that suggested alternative specifications of adjustment variables. In brief, the primary claim was that the effects of school facilities and resources were not clarified by simultaneous adjustment for family background. Instead, parents with high levels of education and the family income to support a wide range of neighborhood choice were likely to choose to send their children to schools with high expenditures. As a result, some of the expenditure “effect” was said to be picked up by the family background coefficients themselves.21
As table 6 shows, this criticism is hard to sustain with the ELS data because the unadjusted relationship between expenditures and educational outcomes is very weak. But a fair critic could reasonably wonder whether some fashion of suppression is in operation and may therefore care to know how models that allow least squares formulae to purge common linear dependence between predictors might generate alternative conclusions. In brief, the answer is: not much at all. Consider just the prediction of tenth-grade math test scores, as for figures 2 and 3. A model that specifies all race-ethnicity, region, urbanicity, and family background variables generates an R-squared value of 0.266, which is smaller than the summation of the separate R-squared values from table 6, which were 0.153, 0.184, and 0.040, respectively. As is well known, these variables share predictive variance for educational outcomes. What is the result when we now add expenditures to this multiple regression specification? Almost nothing. The R-squared value for a model that adds per-pupil salary expenditures remains at 0.266, and the coefficient on expenditures is nonsignificant and substantively trivial. If, instead, we add the student-to-teacher ratio, the percentage of teachers with advanced certification, our four scales of the conditions of facilities, and the principal’s learning “hindered by” scale to the model, the R-squared value increases from 0.266 to only 0.269. And this is the common pattern for all outcomes, with all measures of expenditures and all measures of school characteristics. The unadjusted models reported in table 6 are excessively favorable to the assertion that expenditures and facility differences matter.
Multilevel Models
Since the 1990s, it has been customary to call for multilevel regression models in observational educational research whenever student-level data are nested within school-level data. Figures 5 and 6 demonstrate why the separation of an association into a between-school component and a within-school component can offer an illuminating descriptive portrayal of a relationship. Contrary to what other scholars sometimes imply, multilevel modeling does not in general clarify causal inference; estimating between-school effects and within-school effects at the same time does not imbue either with causal power (see also Lucas’s paper in this issue for a related critique).
For the ELS, the possibilities for multilevel modeling are limited by our comparatively small within-school sample sizes. As a comparison, Borman and Dowling (2010), in their reanalysis of a subset of the original EEO data with multilevel models, utilized a sample of 30,590 ninth-graders enrolled in 226 schools. In contrast, we have a smaller and more dispersed sample at our disposal, with 8,037 tenth-graders enrolled in 559 schools. As depicted in figures 2 and 3, we typically have between 10 and 20 students per school, but the full range is from 3 to 29 students per school. Although one can induce software to estimate multilevel models with samples like the ELS, too little information is available at the school level to reliably estimate both school-level and student-level associations with enough random components to bring the models into alignment with standards in multilevel modeling. And if one wishes to adjust away potential bias from panel attrition and missing data on outcomes using tailored complete case weights, multiple positions exist on how such weights should or should not propagate to school-level associations. Rather than force software to do what we think is unwise, we instead offer some basic between-school models to explain why such an effort would not substantially elevate the explanatory power of expenditures in the ELS data.
Table 7 presents results from twenty-four school-level regression models in which we show the coefficient for each of our six expenditure measures for the prediction of tenth-grade math test scores. The underlying models are specified to mimic the inferences of multilevel models by utilizing precision weights for each school (that is, scaling the underlying weights by the within-school sample sizes in order to give more weight to schools with more precisely estimated means).
The coefficients in the first column of the top panel are from six separate regression models for all 559 schools, and the coefficients in the third column of the top panel are for a corresponding set of six separate regression models that incorporate adjustments for region, urbanicity, and school means of the six family background measures utilized for the individual-level models in table 6. The second and fourth columns present the R-squared values for the models.
At the school level, the six expenditure measures account for very little of the variance of school means of math test scores, as shown in the second column. The metric coefficients suggest that $1,000 increases are associated with very small increments in test scores, between 0.26 and 0.97 points. The particular amount depends, however, on the measure of expenditure, since $1,000 in total expenditures is less proportionally than for instructional salaries (which is reflected in the standard deviations of $2,310 for per-pupil total expenditures versus $882 for per-pupil instructional salaries). Consider the 0.97 and 0.88 in the last two rows of the first column in the top panel. These are the metric slopes for linear regression lines through study design–modeled analogs to figures 2 and 3. A $1,000 shift is associated with increases of 0.97 and 0.88 on the school mean of math tests, which are 0.13 and 0.12 standard deviations of the school-level standard deviation of test scores (for example, 0.97/7.45 = 0.13, and 0.88/7.45 = 0.12). If 0.13 and 0.12 were warranted estimates of causal effects, then they would be small but nonetheless meaningful effects of what would be a substantial $1,000-per-pupil intervention for each school.
For the six models summarized by the third and fourth columns in the top panel, the additional variables explain a great deal of the variation, as should not be surprising from inspection of figure 5. The very small coefficients for expenditures from the first column move uniformly closer to zero (and flip sign for all expenditures without cost adjustments). These twelve models suggest that between-school differences in expenditures do not predict between-school differences in test scores much at all, but school means of our six family background measures are very strongly predictive. The true causal effects of expenditures lie somewhere in between the values in columns 1 and 3 of the table, and as such these columns constitute reasonable bounds on the range of likely true effects of interventions. Multilevel models would reveal the same basic patterns, if we were to offer a full presentation of them.
As is clear from the red lines in figures 2 and 3, the nonparametric regression smooth for math test scores becomes unstable and turns upward at low and high values of per-pupil expenditures, both with and without cost adjustments. It is reasonable to wonder whether between-school regression results would suggest different conclusions if we were to declare these schools outliers and trim the sample to the interior of the distribution of expenditures. Accordingly, for the models reported in the second panel of table 7, we dropped 41 of the 559 schools from the analysis because their per-pupil, cost-adjusted salary expenditures were less than $2,500 or greater than $4,750 (see, for reference, figures 4 through 6). The results for expenditures do not change substantially. If anything, the R-squared values suggest that limiting the sample increased the predictive power of family background relative to expenditures. Because we do not have any principled reason for declaring that the 41 schools that we dropped for the bottom panel are outliers worthy of purging from the population, and because their funding levels are themselves plausible, we favor the complete-sample models presented in the top panel of table 7. However, if we had decided otherwise, our basic conclusions would not change.
We noted earlier, when presenting the individual-level results in table 6, that expenditures may have slightly stronger associations with bachelor’s degree attainment. To assess whether this difference is present for between-school models as well, table 8 presents twelve models structured analogously to those in table 7, but now for rates of bachelor’s degree receipt. The coefficients that are presented have a different scale than for table 7. The outcome variable now varies between 0 and 1 because it is each high school’s proportion of sampled students who obtained a bachelor’s degree by 2012. Most importantly, the R-squared values suggest that expenditures predict bachelor’s degree receipt to a substantial degree.
Metric Coefficients for Expenditure Variables for Separate Between-School Models of Bachelor’s Degree Attainment, With and Without Adjustments for Family Background, Region, and Urbanicity
In particular, for the full sample results in the first panel, a $1,000 shift in salaries for instructional staff is associated with an increase of 6 percent and 4 percent in bachelor’s degree receipt, with the difference between the two attributable to cost adjustment. The results in the third column suggest that simultaneous adjustment for family background differences across schools reduces the net associations by half, to 3 and 2 percent, respectively. The bottom panel offers similar conclusions, after dropping the forty-one schools with low and high levels of expenditures.
What are we to make of this last set of results? For context, we should note that we offer results for the other four outcome variables in supplementary appendix tables S6–S9. The results for the other two test score outcomes are very similar to those already presented for tenth-grade math test scores in table 7. The same is true for on-time high school graduation. However, the results for the rate of any postsecondary education suggest that the predictive power of expenditures, just as one would expect, is midway between the patterns revealed by tables 7 and 8. Similar expenditures predict an increase in the attendance rate of 3 and 2 percent, rather than 6 and 4 percent, for bachelor’s degree attainment. And again, these coefficients are reduced by about half when simultaneous adjustment for school means of family background are used as adjustment variables.
Now to the substantive question: why do we see slightly more predictive power for expenditures in these between-school models of postsecondary educational attainment? Substantively, there may be good reason to believe narratives that stress why long-run outcomes are influenced by learning environments more than is suggested by the analysis of only short-run, test-based outcomes (see Jennings et al. 2015). However, it is not necessarily the case that expenditures explain the divergence. It may be that, even net of family background differences across schools, college-bound youth have parents who choose to send them to more highly resourced schools, under the common belief that schools with more resources are also more likely to prepare their children for college. Students might, in turn, benefit from being surrounded by concentrations of college-bound youth, even if their short-run performance is unaffected (see Wells and Crain 1994). These same parents may also have higher levels of wealth, against which they can borrow to fund their children’s postsecondary education through to bachelor’s degree completion. Our measures of education, occupation, and income do not fully account for wealth differences between ELS families and hence average levels across their schools.
DISCUSSION
We have offered an analysis of standardized test performance in secondary school and subsequent educational attainment for the high school class of 2004, measured from the sophomore year in 2002 through eight years after typical high school graduation. Setting up the results in ways consistent with the organization and design choices of EEO, we first showed that patterns of achievement and attainment are stratified by race-ethnicity and one dimension of ancestry, using a categorization that is consistent with EEO but also updated for use today. We then showed that the profiles of the high schools attended by ELS students—from patterns of segregation through differences in school facilities and maintenance—are not too dissimilar from those that Coleman and his colleagues considered five decades ago. We also showed what is perhaps surprising to some readers: disparities in expenditures that, without adjustment for the higher costs of schooling in metropolitan areas, imply that some of the groups with the lowest achievement attend schools with some of the highest expenditures.
We then offered models—again following some of the study design choices of EEO—that showed how weakly expenditures and facilities predict achievement and attainment for the ELS students. This weak predictive power remained after adjustments for costs and for family background, as well as after robustness checks that redefined the sample (for example, dropping charter and magnet school students from the individual-level models and dropping schools in the tails of the expenditure distributions from the school-level models). For economy of space, we focused the latter part of our school-level analysis on tenth-grade math test scores and bachelor’s degree receipt, but little additional predictive power for expenditures was revealed in our more comprehensive analysis of all six outcome measures analyzed at the individual level, or in additional between-school models presented in the supplementary appendix.
Altogether, the results are mostly in line with the whispered result that has become the apocryphal characterization of EEO: “It’s all family.” This is certainly what we found for our models of test scores, which were the outcomes studied for EEO. Our between-school models, however, did offer a bit of evidence for expenditure effects on postsecondary educational attainment, especially bachelor’s degree receipt. But even here, the associations were dwarfed by the impressive predictive power of between-school means of our measures of family background.
But why? In the remainder of this section, we first discuss contrarian methodological explanations that are plausible. We then consider substantive explanations, based on extant research.
Contrarian Explanations for Why the Results May Be Artifactual
As is always the case in observational research with imperfect data, explanations for the patterns of results exist that justify dismissing them on methodological grounds. These explanations include:
Expenditures measured at the district level are a poor indicator of the expenditures relevant to the instruction of individual students, as discussed at the beginning of this paper. As a result, the measured variables we utilized have too little validity to sustain inferences of little or no causation from models that demonstrate little or no association.
The ELS sample, and perhaps all of its predecessors since EEO, departs systematically from the target population of regular public high schools in the United States. Schools with students who are harmed by the low expenditures of their districts do not agree to participate in the survey at the same rate as other schools.
Because the ELS sample was drawn in the spring of the sophomore year, a disproportionate amount of variation relevant for the relationships between expenditures and outcomes is absent. Students whose outcomes would generate stronger positive relationships between expenditures and test performance and between expenditures and educational attainment dropped out of high school before the sample was drawn.
Although we concede that these explanations are plausible, we think that they are too extreme, for the following reasons.
For the first explanation, it is undoubtedly the case that there are many school-to-school variations in expenditures. Nonetheless, with nearly fifty years to investigate this possibility since scholars such as Christopher Jencks (1972) first tried, we know of no research that has uncovered stronger effects on achievement for within-district, school-by-school differences in per-pupil expenditures. It is possible that school-to-school variation is not predictive because it is generated mostly by the minor lumpiness of class sizes, slight variation in teacher salaries due to seniority, and other patterns that have little bearing on learning processes. Studies such as Archibald (2006) are largely uninformative because they do not have sufficient measures of students’ family backgrounds, and those such as Odden et al. (2008) are focused on the costs of specialized interventions in small numbers of schools—again without sufficient student-level measures of parent characteristics and home environments.
We should also note that some of our results are incompatible with this explanation. The ELS includes ratings of school facilities that capture their condition and maintenance, and these are measured directly at the school level by the relevant ELS survey administrator. Our results match those of Bowers and Urick (2011) in showing that these measures have very small associations with outcomes in the ELS: they explain no more than 2 percent of the student-level variance, even without adjustments for differences in family background. In addition, the ELS elicits items for a scale of whether school principals felt that the learning of tenth-graders was “hindered by” school facilities and their condition. This scale predicts outcomes even more weakly.
These arguments aside, we think that there may well be a relevant hidden dimension across schools that our measures of expenditures cannot pick up: the apparent desire, on average, of many teachers to work in environments, for similar salary levels, where students are easier to teach. We discuss sorting of this type later, because it may be part of a true substantive explanation for our results.
Moving to the second potential methodological explanation, it is possible that patterns of cooperation with NCES vary in ways that undermine the results of longitudinal surveys such as the ELS. The nation’s education data collection apparatus does not allow for enough linking of our national samples to universe characteristics of outcome distributions that would permit evaluations of this sort of explanation. Thus, while we know of no evidence that supports this explanation, we also wish that evidence to refute it were available.
More work is needed to conclusively eliminate the third explanation as well. Parallel analyses such as ours for elementary and middle schools would be helpful. Surely more work could be done with national data sources, and we are surprised that we could not find more studies structured just like ours, including some for elementary school students. It is possible that such studies do exist but that they are unpublished because of the “recycling bin” effect that too frequently consigns null findings to the paper mill. Only in celebrations of the EEO, such as this one, are publication goals clearly in line with demonstrating a set of findings that might otherwise be dismissed by journal referees as null results that need not be published.
Positive Substantive Explanations
As much as we find the methodological explanations of the last section unpersuasive, we cannot eliminate them from plausibility. But suppose for this section that they are invalid. And furthermore, suppose that our results are even more extensive, such that they would hold even for measures of standardized test performance and grade progression in elementary and middle school as well. This extended supposition, as we noted earlier, may be incorrect, but too little research has focused on associations between expenditures and educational outcomes in elementary and middle school for us to know. For the sake of argument, suppose that such additional research would come into line with the basic patterns revealed in this paper.
In this case, any substantive explanation can, first and foremost, avail itself of decades of research that suggests why family background is a fundamental cause of educational outcomes. Many of these explanations can account for both between-school and within-school differences in outcomes. We will not review this literature because many pieces already exist that show its connections to the arguments of EEO (see Gamoran and Long 2007; Sørensen and Morgan 2000), as well as other papers in this issue (see Alexander’s paper in particular).22
Beyond the large explanatory component attributable solely to the pervasive effects of family background, a full substantive explanation of our results would benefit from two additional components, one of which would explain why expenditures have always had weak associations with outcomes and the other of which would explain why those weak associations may have declined over the past five decades.
If one believes the recent research that argues that (a) teacher effectiveness varies a great deal and (b) sorting exists, such that highly effective teachers, at every salary level, are the least likely to be working in regular public schools with the most disadvantaged students, then it follows that instructional quality may have a weak association with average teacher salaries. And because teacher salaries are a large component of differences in expenditures across districts, all measures of expenditures may have correspondingly weak associations with educational outcomes. This structure of teaching effectiveness, generated by the choices of teachers and those who hire them, may have lurked beneath the EEO data as well.
Consider the literature on teacher sorting, which is a prominent theme in decades of research on teacher mobility and teacher attrition. As early as Becker (1952), it has been recognized that many teachers favor work conditions that do not require that they teach students with substantial home disadvantages, or as Howard Becker wrote after studying public schools in Chicago:The positions open to a particular teacher in the system at a given time appear, in general, quite similar, all having about the same prestige, income, and power attached to them. . . . Though the available teaching positions in the city schools are similar in formal characteristics, they differ widely in terms of the configuration of the occupation’s basic work problems which they present. . . . The greatest problems of work are found in lower-class schools and, consequently, most movement in the system is a result of dissatisfaction with the social-class composition of these school populations. Movement in the system, then, tends to be out from the “slums” to the “better” neighborhoods, primarily in terms of the characteristics of the pupils. Since there are few or no requests for transfer to “slum” schools, the need for teachers is filled by the assignment to such schools of teachers beginning careers in the Chicago system. Thus, the new teacher typically begins her career in the least desirable kind of school. (Becker 1952, 471–72)
Subsequent research in the wake of EEO reinforced Becker’s point that salary differences were not the crucial determinant of such moves (see Greenberg and McCall 1974). A consensus position emerged that teachers appeared to demand higher wages to teach in schools with concentrations of students living in poverty, especially if those students were nonwhite (see Antos and Rosen 1975 and Levinson 1988, both of which use EEO as motivating material). More recent research suggests that these patterns remain (see, for example, Clotfelter, Ladd, and Vigdor 2011; Goldhaber, Destler, and Player 2010).
If the realities of dysfunction in distressed urban districts are now as dire as scholars such as Charles Payne (2008) claim, then teacher sorting patterns may have strengthened since the 1960s.23 Moreover, the accountability and standards movement has made it clear to teachers how very risky it is for their career prospects to teach students whose learning is undercut by disadvantages in the home (see Labaree 2010). It would be hard to imagine effective teachers not sorting themselves more than ever in ways that would reinforce any preexisting pattern, even if more teachers are now motivated to enter the profession for altruistic reasons than they were before the challenges of contemporary schooling became widely known and publicly debated.
If one does not believe the recent literature on teacher effectiveness, arguing instead that differences in teacher effects are modest and do not cumulate to the school level, then sorting by teachers may still exist so that salary rates, and hence expenditures, are more similar across districts than would otherwise be the case. And if teachers have comparatively small effects, perhaps because the influences of families are so strong, learning outcomes would then have to be largely determined by support from the home and experiences in residential neighborhoods. In this case, differences in expenditures across districts may reflect sorting by teachers, with higher salaries in more distressed and demoralized districts being necessary simply to staff the classrooms, conditional on differences due to years in the teaching profession.
Regardless of what position one takes on the distribution of effective teachers, it must still be recognized that all of the changes in the structure of inequality and in the policy landscape discussed at the beginning of this paper are in the direction of eliminating any small association between expenditures and outcomes. If Sean Reardon (2011) is correct, and we are witnessing since the 1980s a strengthening of the effects of family background on educational outcomes for a variety of reasons, then both within-school and between-school associations between socioeconomic status and educational outcomes may be rising.24 But more than this, it is likely that federal funding for compensatory education programs, coupled with states’ foundation funding, have delivered funding precisely where it is thought to be needed, so that schools that struggle to generate positive results are also schools that increasingly receive resources that can, it is hoped, help to meet their challenges. But herein has been the opening for the education reform movement. Many of its proponents argue that these additional resources of recent decades have encountered demoralization and dysfunction, which are part and parcel of a preexisting regime of sorting by teachers, and perhaps also by school leaders. If this explanation has merit, then it is the alternative solutions that must continue the debate. Either policy must fundamentally transform schools, or it must deliver an unprecedented amount of money to undo the sorting of effective teachers and school leaders. Either possibility could be successful, although the proponents of each strategy are likely to lock horns.
The more frightening possibility, which we cannot dismiss, is that effective teaching does not line up with the sorting of teachers and all of the most important determinants of educational outcomes remain in the home. In this case—which is probably the default position of many sociologists of education—redistributing teachers and school leaders, by whatever method is feasible, would have small effects on the distribution of outcomes. In this case, only a reduction of the inequality of life conditions into which children are born can generate a meaningful reduction in the inequality of educational outcomes that concerns us all.
Acknowledgments
We thank Joel Pally for his assistance in graphing the faux ELS.
FOOTNOTES
↵1. See Carver (1975) for an early version of the argument, as well as Jencks (1972) for an early attempt to evaluate it. For the most widely read account, see Kozol (1992), which almost completely ignores the extant literature. See Archibald (2006) and Odden et al. (2008) for newer pieces in line with this argument, although motivated by the important goal of developing viable school-level resource measures.
↵2. For an early explanation of the argument, see Cain and Watts (1970) as well as the response by Coleman (1970). See Card and Krueger (1992, 1996) for discussion of the most heavily regarded attempt to support it by adopting an alternative design using state-level variation. See Nguyen-Hoang and Yinger (2014) for a recent attempt to sustain it by adopting a related approach.
↵3. See figure 21.1 in Corcoran and Evans (2015), which depicts real growth in expenditures from local, state, and federal sources. While expenditures from all sources have increased substantially since the 1960s, the growth of state funding is the most substantial.
↵4. Grubb’s (2009) expanded resource categories are divided into what he calls compound, complex, and abstract resources. Some of his choices are, we think, nonsensical. For example, he demonstrates how students’ curriculum track placements strongly predict many educational outcomes (see his table B1), and he takes the position that track placements should be labeled a compound resource for a school. Decades of research demonstrate that family background strongly predicts track placement. Putting the predictive power of track placement in the column of a school resource effect rather than a mechanism for family background advantage or disadvantage is puzzling. In general, Grubb’s semantic shift does not change the associations for expenditures, nor the endogeneity of his additional types of resources relative to family background.
↵5. Baker (2012, 1) appears to argue that their claim about the presence of larger school effects in the EEO data supports the inference that the effects of resource differences were larger than Coleman and his colleagues inferred. He cites a sentence from the abstract of Borman and Dowling (2010), without follow-up, and without noting that Borman and Dowling lack the expenditures measure that EEO and the early replications utilized. In fact, Borman and Dowling show that the “school” differences they reveal are largely due to average family background differences across schools.
↵6. The intervention is clearly in line with the call for experimentation, perhaps first issued by John Gilbert and Frederick Mosteller (1972).
↵7. It is a school that when sampled was revealed to be a school solely in a local education agency (LEA) for special needs students, with very large per-pupil expenditures but medium-to-low educational performance.
↵8. The race-ethnic categories used for EEO were “Mexican American,” “Puerto Rican,” “Indian American,” “Oriental American,” “Negro,” and “Majority or white” (see Coleman et al. 1966, 10, table 1, and throughout).
↵9. Non-Hispanic American Indian and Alaskan Native students attended schools that, on average, appeared similar to those attended by white non-Hispanic students. However, there are additional measurement complications for these students, owing to their clustering within a few schools in the ELS as well as the complex multiple racial identities expressed by students not in these few schools. We will therefore devote comparatively little attention to interpreting the patterns for these students.
↵10. The acronym NHOPI, which applies to some respondents in the broad category we label “Asian” in the text, is the U.S. 2000 census label for “Native Hawaiian or Other Pacific Islander.”
↵11. Of particular importance for comparisons to EEO, many Hispanic respondents who self-identified as black or African American are embedded within our category “Hispanic ethnicity other than Mexican, all generations.” “Puerto Ricans” were their own category for EEO, alongside “Mexican Americans.” One wonders about the definitions of these groups for EEO, as well as the heterogeneity within them (and within the “Majority or white” group as well).
↵12. For the comparisons of the conditions of classrooms, hallways, and bathrooms, the differences in the group-specific standard deviations are typically on the order of 1.2 versus 0.8. For the areas around schools, the differences are larger for blacks and Hispanics who did not claim Mexican ancestry relative to non-Hispanic whites (typically 1.6 versus 0.6). For Hispanic students who claimed Mexican ancestry, the differences are smaller (typically 1.0 versus 0.6).
↵13. The most common measurement approach when assessing expenditure differences is to use total current expenditures to form comparisons. The results of this paper are essentially the same if we use this measure, but we favor the alternatives presented in table 5. Instructional expenditures are the core expenditures for learning within the total current expenditure measure, and instructional expenditures are defined for the CCD as “includes payments from all funds for salaries, employee benefits, supplies, materials, and contractual services for elementary/secondary instruction; excludes capital outlay, debt service, and interfund transfers for elementary/secondary instruction. Instruction covers regular, special, and vocational programs offered in both the regular school year and summer school; excludes instructional support activities as well as adult education and community services” (Berry and Zhou 2007, B-6). Salaries are then a subset of this measure. The more encompassing measure of total current expenditures, which we do not utilize, includes expenditures for instructional support services, expenditures for administrative support services, food services, maintenance services, and others. We see more rationale for moving right past total current expenditures and instead taking all expenditures into account when looking to complement an analysis based only on instructional expenditures and instructional salary expenditures. The CCD measure of total expenditures includes everything in total current expenditures, but also capital outlay, which includes expenses for construction and equipment (including instructional equipment). Thus, we see the total expenditures measure as close to the value that many parents recognize implicitly when choosing schooling options based on residential location, while expenditures on instruction is a targeted measure of the resources allocated to the instruction of the modal pupil in each school district. Finally, we use a four-year average, which smooths out the variation in capital outlay across the years (which is thought to be more volatile than expenditures for instruction). Recall also that the expenditure measures are for each district as a whole, not individual schools, and so the capital outlay in each year is itself averaged across all schools.
↵14. We do not adjust for price differences across the four years and simply take the average of the slightly escalating values across the four years. We assume that variation attributable to local inflation rates is ignorable, and thus that our four-year averages work well for the level of expenditures experienced by students sampled near to the midpoint of their high school careers (the spring of sophomore year, when the 2002 ELS was fielded).
↵15. We cannot offer a map that displays the actual ELS schools, for disclosure reasons, but we assure the reader that the one in figure 1 looks qualitatively similar. Slightly different schools are chosen in each metropolitan area, but they are all represented in about the same proportions as in figure 1. More variation is present, as expected, for nonmetropolitan areas, but the overall pattern for the true ELS schools is qualitatively similar to figure 1 when viewed at the presented scale. The optimal way to view the figures in this article is in color. We refer readers of the print edition of this paper to www.rsfjournal.org/doi/full/10.7758/RSF.2016.2.5.05 to view the color version.
↵16. Supplementary appendix figure S1 shows an analogous map for the underlying wage and salary data. Figure S1 is more dispersed by color, with high-wage counties in and near San Francisco and New York City especially pronounced. Shrinking the averages to the national median brings these high-salary metropolitan areas into closer alignment with other metropolitan areas. A similar pattern is present for the other end of the distribution (for example, for Appalachian counties relative to other rural counties).
↵17. Technically, these variables are measured at the school level, and some students live in urban areas but attend schools in suburban areas, and so forth. But these are not separable without students’ residence locations, which are not available for the ELS. Nonetheless, most students live in areas that match their schools, when measured at this geographic scale.
↵18. This scale is a factor-weighted composite of ten items that the school principal rated on a four-point scale from “not at all” to “a lot” in response to the question: “In your school, how much is the learning of tenth-graders hindered by: (a) poor condition of buildings, (b) poor heating, cooling, or lighting systems, (c) inadequate science laboratory equipment, (d) inadequate facilities for fine arts, (e) lack of instructional space (for example, classrooms), (f) lack of instructional material in the library, (g) lack of text books and basic supplies, (h) not enough computers for instruction, (i) lack of multi-media resources for instruction, and (k) inadequate or outdated vocational-technical education equipment or facilities.” Item j (“lack of discipline and safety”) was excluded from the scale, as it did not fit with the first factor.
↵19. We offer in supplementary appendix table S5 all models in table 6 estimated with OLS regression. As such, the models for educational transitions become linear probability models. We also report adjusted R-squared values (instead of unadjusted R-squared values for test scores and Tjur’s [2009] coefficient of discrimination for the educational transition models). The results are nearly the same, and all of this paper’s conclusions would be the same substituting those models into the main text.
↵20. The results in figures 2 and 3, as well as those in figures 4 through 6, do not account for the study design of the ELS; for example, they do not incorporate adjustments for the nested sample design or nonresponse. We offer these figures only to provide a sense of the main patterns in the data that shape the more carefully estimated results in the tables.
↵21. Although Coleman and his colleagues could not deflect this criticism effectively (see Coleman 1970), compelling evidence against the criticism was present in the EEO data all along, as shown in replications such as Smith (1972; see his appendix tables). The unadjusted relationship between expenditures and test scores was very weak, and hence the adjustment for family background inputs was not crucial to the conclusion that the estimated effects of expenditures were surprisingly small. Coleman and his colleagues could have blunted this particular criticism if they had simply shown the bivariate associations between expenditures and outcomes, rather than revealing associations only conditional on family background adjustment. In fact, it is clear to a contemporary reader that one of the main weaknesses of EEO was its overreporting of results in table after table, many of which muddied the waters with variance comparisons across alternative specifications of models that were not always clearly conveyed in the writing.
↵22. In addition, we think the support for “school” effects in Grubb (2009) and Borman and Dowling (2010) is also consistent with the extant research because the relevant coefficients in their models are best interpreted as endogenous with respect to family background as well.
↵23. In addition, some struggling school districts are plagued by dysfunction between state officials, local elected officials, and school administrators. This dysfunction often generates haggling over funding allocations. Such dysfunction can lessen the effectiveness of the available resources that are eventually distributed and recorded as expenditures. In addition to generating staffing uncertainty that undermines program effectiveness, teachers and administrators may be more likely to flee to external opportunities that are more stable and compatible with their long-term career goals.
↵24. Certainly, we know of no evidence that suggests that these gaps are closing. Results from the long-term assessments for the National Assessment of Educational Progress (NAEP), for example, show remarkable consistency in test score results across levels of parents’ education.
- Copyright © 2016 by Russell Sage Foundation. All rights reserved. Printed in the United States of America. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Reproduction by the United States Government in whole or in part is permitted for any purpose. We thank Joel Pally for his assistance in graphing the faux ELS. Direct correspondence to: Stephen L. Morgan at stephen.morgan{at}jhu.edu, Department of Sociology, 3400 N. Charles St., Johns Hopkins University, Baltimore, MD 21218; and Sol Bee Jung at sjung26{at}jhu.edu, School of Education, 2800 N. Charles St., Johns Hopkins University, Baltimore, MD 21218.
Open Access Policy: RSF: The Russell Sage Foundation Journal of the Social Sciences is an open access journal. This article is published under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.